| |
|
|
Eine naive Implementierung der Hausdorff-Distanz kann wie folgender Pseudocode aussehen:
float a_to_b = 0
float b_to_a = 0
for all x in A
for all y in B
if euclidean(x,y)> a_to_b
then a_to_b=euclidean (x,y)
for all y in B
for all x in A
if euclidean(y,x)> b_to_a
then b_to_a=euclidean (y,x)
return max(a_to_b, b_to_a)
Allerdings lässt sich die Laufzeit von O(n²) dieser Implementierung durch eine effizienter gestaltete Suche deutlich verbessern, wie im Abschnitt über den KD-Baum erläutert wurde.
Diskussion der Distanzfunktion
Die Euklidische ist nicht die einzige mögliche Metrik, wenn es um die Umsetzung der Hausdorff-Distanz geht.
Im Laufe der Implementierung wurde auch die Manhattan-Metrik testweise verwendet. Als diese nur einen minimalen Laufzeitvorteil erreichen konnte, verwarf ich diesen Ansatz jedoch wieder, da ich die euklidische Distanz bei Abständen im 3-Dimensionalen als intuitiver empfinde.
Zur Implementierung wurde die Bibliothek nanoflann verwendet.
Diese implementiert eine sehr allgemeine, gut optimierte KD-Baumstruktur, welche an die speziellen Bedürfnisse des Nutzers angepasst werden muss.
Sie ist sowohl für Anfragen nach einem einzigen, aber auch für Anfragen nach mehreren nächsten Nachbarn (innerhalb eines Radius um den Anfragepunkt oder der k nächsten Nachbarn) geeignet.
Die Hausdorff-Distanz selbst liefert einen einzigen Ausgabewert, der als größter Abstand zwei nächster Nachbarn keine allzu großen Aussagen über die Deckungsgleichheit der Meshes erlaubt. Daher wurde der Abstand zum nächsten Nachbarn verwendet, um eine punktweise Einfärbung der Meshes zu erstellen. Mehr dazu weiter unten.
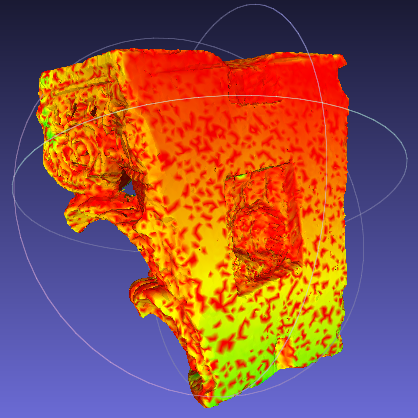Nachdem eine effizientere Laufzeit erreicht worden war, zeigten die Meshes noch immer an Stellen Ausreißer, an denen glatte Flächen vorlagen und somit die suggerierte hügelige Oberfläche nicht zu finden sein konnte.
Das Problem wurde als Berechnung einer Punkt-zu-Punkt-Distanz erkannt. Da die Meshes unterschiedlich viele Punkte besitzen, kann es vorkommen, dass die Abstände zwischen zwei Punkten relativ groß sind, obwohl die angrenzenden Facetten (Oberfläche des Meshs) nicht allzu weit voneinander entfernt sind.
Die Lösung bestand darin, den nächsten Nachbarn zu finden und die Abstände zwischen dem Anfragepunkt und seinem nächsten Nachbarn, sowie die an diesen angrenzenden Facetten zu bestimmen. Der minimale Wert dieser Menge wurde als Abstand vom Anfragepunkt zum anderen Mesh übernommen.
Jede Facette, die den nächsten Nachbarn berührt, spannt eine Ebene auf. Um den Abstand eines Punkts zu einer Facette zu bestimmen, wird zunächst der Anfragepunkt in die Ebene projiziert, die von der Facette aufgespannt wird. Nun wird mit Hilfe der HNF der Abstand zwischen dem Anfragepunkt und seiner Projektion berechnet.
Da eine Facette im Gegensatz zu der von ihr aufgespannten Ebene begrenzt ist, muss noch überprüft werden, ob die Projektion tatsächlich innerhalb der entsprechenden Facette liegt.
Um dieses Problem mit möglichst wenig Aufwand zu lösen, wurden baryzentrische Koordinaten verwendet. Da die betrachteten Meshe ausschließlich dreieckige Facetten besitzen, kann diese Methode für jede Facette genutzt werden.
Werte, die von Projektionen stammen, welche nicht in der benachbarten Facette liegen, werden verworfen. Das Minimum der verbleibenden (einschließlich der Punkt-zu-Punkt-Distanz), ist der gesuchte Abstand.
Die Grundidee der baryzentrischen Koordinaten ist die Tatsache, dass sich jeder Punkt in der Ebene eines Dreiecks als Linearkombination der Vektoren zwischen jeweils zweier Eckpunkte des Dreiecks beschreiben lässt:
P = A + u*(B-A) + v*(C-A)
Ist eine der Variablen negativ oder größer als eins, so liegt der Punkt garantiert außerhalb des Dreiecks.
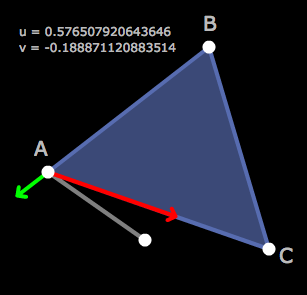
Sind u und v größer oder gleich Null und kleiner als Eins, ihre Summe jedoch größer als Eins, so liegt der Punkt ebenfalls nicht im Dreieck – man ist über die Linie zwischen B und C hinausgelaufen.
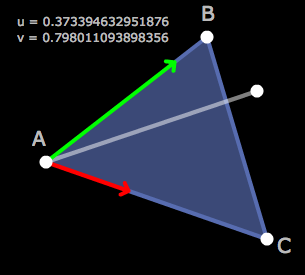
Im verbleibenden Fall (u,v ≥ 0 und u+v ≤ 1) liegt der Punkt im Dreieck.
(Siehe auch: Blackpawn.)
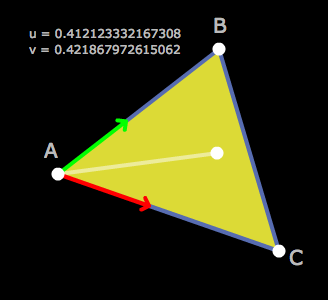
Die Stärke dieser Methode liegt in ihrer einfachen Berechenbarkeit – eine Linearkombination und höchstens drei Vergleiche sind nötig, um zu bestimmen, ob ein projizierter Punkt innerhalb einer Facette liegt.
Dies ist numerisch einfacher zu berechnen als eine Winkelbetrachtung und weniger aufwändig als ein Vergleich, auf welcher der Dreiecksseiten ein Punkt liegt.
Zu Testzwecken wurde die Software auf zwei ineinandergeschobene Elipsoide, erstellt von Andreas Beyer, angewendet. Diese werden im folgenden Abschnitt verwendet werden, um die Veränderung der Farbgebung zu verdeutlichen, da sie daran intuitiver ersichtlich ist, als an den Kapitellen.
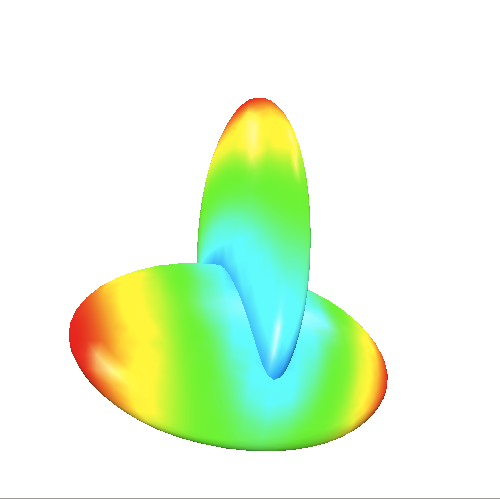Der erste Ansatz zur farblichen Darstellung der Abstände war eine symmetrische Verteilung der Farbwerte von rot zu blau, wobei die Extrema rot bzw. blau eingefärbt wurden.
Die Überlegungen zum dabei verwendeten "Colour Cube" finden sich hier unter dem Stichpunkt 'Colour Ramping for Data Visualisation'.
Die so erzeugte Farbverteilung entsprach nicht dem gewünschten Ergebnis, nämlich: rot für Überschneidungen des anderen Meshs, blau für seine Unterschneidungen und grün für Übereinstimmung der Meshes.
Am augenfälligsten ist rechts, dass die grüne Farbe sich nicht im Bereich des Schnitts der Ellipsoide befindet.
Symmetrische Ansätze
Der nächste Schritt bestand im Festlegen der grünen Farbe auf die Distanz null.
Doch wie sollten die restlichen Werte verteilt werden? Da noch immer von einer symmetrischen Farbgebung ausgegangen wurde ergaben sich zwei Möglichkeiten:
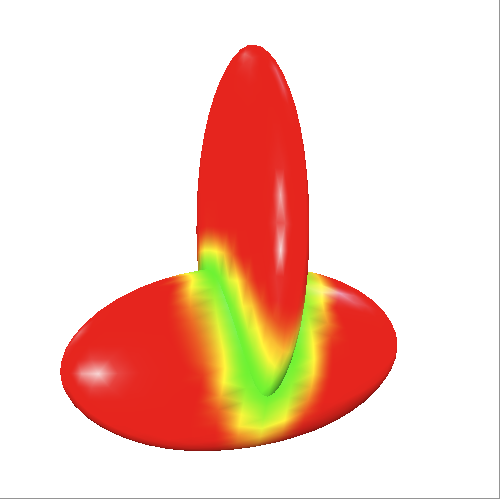1) Festlegung des farblichen Extremums (also rot oder blau) auf den betragsmäßig kleineren Extremwert.
Daraus folgte eine Farbgebung, bei der - wie im nebenstehenden Bild zu sehen - bei allzu großer Differenz zwischen größter Über- und Unterschneidung zu schnell der farbliche Extremwert für die andere Seite der Farbskala erreicht wird. Dies ist einerseits nicht wünschenswert, da offensichtlich Informationen bezüglich des konkreten Abstands verloren gehen, und andererseits, da durch die vielen scheinbaren Extrema der Eindruck entsteht, Der Abstand der Meshes sei sehr groß.
2) Festlegung des farblichen Extremums auf den betragsmäßig größeren Distanzwert. Dies hatte zur Folge, dass dem betragsmäßig kleineren Extremum nie der farblich mögliche Extremwert zugewiesen wurde. Somit wurde ein Teil der möglichen Farbskala verschwendet. Weiterhin zog dieser Ansatz den störenden Effekt nach sich, dass die "betragsmäßig kleineren Extrema" kaum als solche wahrgenommen wurden.
Divergente Lösung
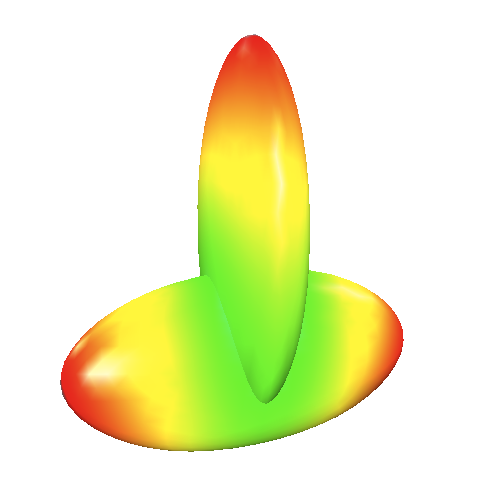Als Lösung wurde schließlich eine divergente Farbskala gewählt.
Das heißt, dass die grüne Farbe auf die Distanz Null festgesetzt wurde. Die größte Überschneidung wurde rot eingefärbt und die weiteren überschneidenden Punkte wurden entsprechend der oben verlinkten Methode auf die Farbskala rot-gelb-grün abgebildet. Analog wurde mit den Unterschneidungen verfahren.
Die Grafik unten zeigt deutlich, dass die so generierte Farbgebung nicht symmetrisch ist.
Ein als größte Überschneidung markierter Punkt ist also nicht zwangsläufig genauso weit vom anderen Mesh entfernt, wie die größte Unterschneidung.
Es bestand die Annahme, dass die volle Ausnutzung der Farbskala sinnvoller wäre, als eine der oben beschriebenen symmetrischen Vorgehensweisen, da es ohnehin notwendig werden würde, eine Legende zu implementieren oder zumindest die Abstände der größten Über- und Unterschneidungen auszugeben.
Ausreißer
Bei der Betrachtung der Meshes zeigte sich, dass die größten Ausreißer deutlich größer als der mittlere Abstand der Meshes waren. Dies hatte eine wenig aussagekräftige Färbung zur Folge, da teilweise fast die gesamte Farbskala auf einzelne Ausreißer verwendet wurde.
Daher wurde die Entscheidung gefällt, ein Quantil anzulegen.
Dieses wurde umgesetzt, indem jeweils die n Punkte verworfen wurden, die am meisten über- bzw. unterschnitten. 'n' bezeichnet in diesem Fall ein Prozent der Gesamtzahl an Punkten. Insgesamt wurden also zwei Prozent der Messwerte verworfen und zur Verdeutlichung grau gefärbt.
Der Wert von zwei Prozent hat sich für die gegebene Situation als passend herausgestellt, für andere Meshes werden andere Werte geeigneter sein.
Zurück - Nach oben - Weiter
|
|
|
