
|
|
|
The Hopf map |
|
Stereographic projection |
|
How all works together |
|
Algorithms |
|
|
||||
The Hopf map |
||||
| The Hopf map is a in many regards very
interesting continuous map from the four-dimensional 3-sphere to the
ordinary 2sphere (see also David Lyon's article, from which much of what I'm saying is
drawn). Heinz Hopf discovered (or invented, depending on the point of
view your prefer) it at the beginning of the 19th century while
studying questions in topology, more precisely: homotopy
theory. His discovery represented a great breakthrough in the field. We will not go into details here but rather examine its use for our purpose. The map is defined as follows: 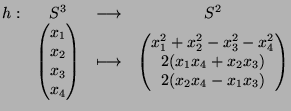 Its topological properties are outstanding and reveal much of the sphere's structure, which is why it fits our purpose very well. As mentioned above, the Hopf map (subsequently simply referred to as "h") is continuous and surjective. The latter property means that we can obtain the whole of the hypersphere S3 as preimages of points on S2. In particular, the preimage h-1(P) of a point P(p1,p2,p3) on S2 is a circle. Such a circle obtained as the preimage of a point under the Hopf map will be called a "Hopf circle". Its parametrization is given by 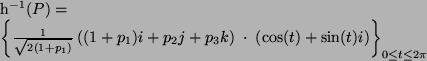 Here i, j, and k denote the basis vectors (other than 1) of R4 interpreteted as the algebra of quaternions, and the multiplication dot indicates quaternion muliplication. If we multiply this out, we obtain the following explicit parametrization in vector form: 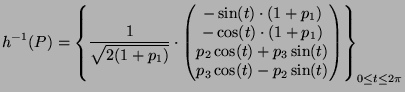 Some short calculations confirm that this is the parametrization of a circle obtained from the unit circle in the complex plane (embedded in R4) by a certain rotation. It is a most astonishing fact that for any two points P and Q on S2 the corrseponding Hopf circles h-1(P) and h-1(Q) are linked, which is why the resulting images possess an intrinsic beauty. Now, instead of only considering preimages of points, we will consider preimages of whole sets on S2. The simplest such sets are circles on S2. These can easily be specified by their plane of intersection with S2 (which is exactly the method of choice in HyperView). The preimage of a circle on S2 turns out to be a torus on S3. When projected into R3, this yields a Dupin cyclide that can finally be visualized (looking like a strangely deformed torus as in the screenshots). This procedure is explained in more detail in the following two sections
| ||||
|
|
© 2003 by Maximilian Albert • Anhalter42@gmx.de