Wiiheadtrack works with two kinds of coordinates/positions.
This section describes how Wiiheadtrack handles these different positions.
The first step is to find out the user's position in front of the Wiimote-camera. This position is called eye-position, because the IR-LEDs symbolize the user's eyes. So the terms eye and IR-LED are used synonymously. The Wiimote-camera captures an image of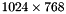 
px. Wiiheadtrack uses the center Wiiheadtrack::eyeC between the eyes (Wiiheadtrack::eyeL and Wiiheadtrack::eyeR) as the initial point of his computations. You can imagine the captured image of the Wiimote as an "imaginary screen" detecting the user's position:
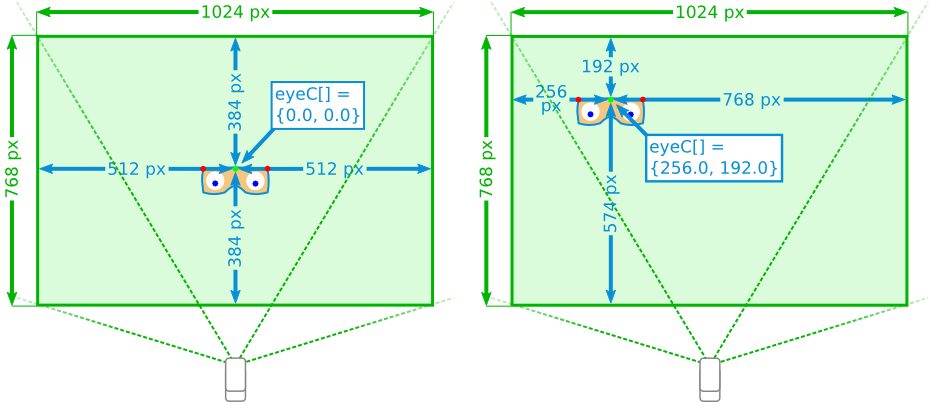
The image shows the imaginary screen from the Wiimote's point of view. You can see the user wearing glasses with two IR-LEDs (red) and eyeC (green). Independent from the distance between the user and the Wiimote-camera, eyeC represents the coordinates of the user at the screen, with the origin at the center of the screen and ![$ \texttt{eyeC} \in [-512.0, 512.0] \times [-384.0, 384.0] \subset \mathbb{R}^2$](form_4.png)
. From the user's point of view, the sign of the x-coordinate is inverted.
The distance between the user and the Wiimote-camera Wiiheadtrack::eyeZ is directly detected by the Wiimote. Because this distance is computed by the distance between Wiiheadtrack::eyeL and Wiiheadtrack::eyeR, it depends on the installation of the IR-LEDs.
Background: As explained, Wiiheadtrack::eyeC is computed with the help of Wiiheadtrack::eyeL and Wiiheadtrack::eyeR, which are detected by the Wiimote-camera:
![\begin{eqnarray*} \texttt{eyeC[0]} &=& ((\texttt{eyeL[0]}+\texttt{eyeR[0]}) \cdot 0.5)-512 \\ \texttt{eyeC[1]} &=& ((\texttt{eyeL[1]}+\texttt{eyeR[1]}) \cdot 0.5)-384. \end{eqnarray*}](form_5.png)
Actually, the origin is placed in the lower left corner of the imaginary screen (from the users point of view) and ![$ \texttt{eyeC} \in [0.0, 1024.0] \times [0.0, 768.0]$](form_6.png)
. For further processing, eyeC is translate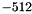d ( 
and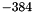 
), so the origin is set to the imaginary screen's center.
Because eyeC is computed by eyeL and eyeR, it is actually impossible for eyeC to reach the left or right border of the imaginary screen. In this case eyeL or eyeR would be outside the screen and eyeC could not be computed. This problem is solved by adding an "offset" from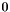 
to ![$0.5 \cdot (\texttt{eyeL[0]} - \texttt{eyeR[0]})$](form_10.png)
from the screen's center to the left or right border:
![\begin{eqnarray*} \texttt{eyeC[0]} &=& \texttt{eyeC[0]} + \frac{\texttt{eyeC[0]}}{512} \cdot 0.5 \cdot (\texttt{eyeL[0]} - \texttt{eyeR[0]}) \\ \texttt{eyeC[1]} &=& \texttt{eyeC[1]} + \frac{\texttt{eyeC[1]}}{384} \cdot 0.5 \cdot (\texttt{eyeL[1]} - \texttt{eyeR[1]}). \end{eqnarray*}](form_11.png)
The second step is to map the eye-position to a (virtual) position Wiiheadtrack::pos (in the following "position") in the 3-dimensional space. The computation depends on the sensitivity and the mode, you work with. Both ways are explained in the context of sensitivity.
1.7.1
