Das hier dokumentierte Praktikum "ILATO - Cmm2Cad" aus dem Sommersemester 2015 wurde von Nicolas Braun durchgeführt und von Andreas Beyer und Susanne Krömker betreut. Als Teil des des Ilato Projektes soll es dazu dienen um Messdaten in ein wireframe Modell zu konvertieren.

Motivation

Im Zuge einer Messung mittels eines Lasers können Werkstücke in der Hesseschen Normalenform (HNF) repräsentiert werden (siehe Fig. 1). Diese enthält jedoch nicht alles relevanten Daten, unter anderem keine Informationen über die Kanten des Objektes. Diese gehören jedoch zu einer im 3D Bereich üblichen Darstellung eines Objektes als wireframe Modell. Es gilt also die benötigten Informationen aus den gelieferten Daten zu schlussfolgern.

Das Datenset

Die Eingabedaten bestanden aus einem Set an Ebenen in der Form von zwei Vektoren, die einen Punkt und seine Normale darstellen (HNF), sowie ein Skalar, das die Qualität der Messung beschreibt siehe Fig. 2. Die Messqualität wird in der momentanen Implementation im fertigen Objekt nicht repräsentiert.

Überblick

Der Algorithmus arbeitet in mehreren Schritten. Zunächst werden alle Schnittpunkte aller Ebenen berechnet (siehe Fig 3). Die möglichen Flächen, die durch die Kombination aller entstehenden Kanten definiert werden (siehe Fig 4), werden dann mittels einer Tiefensuche nach einer validen Kombination durchsucht. Der Algorithmus ist auch im folgenden Video visualisiert:

Video Link

Auffinden der Schnittpunkte

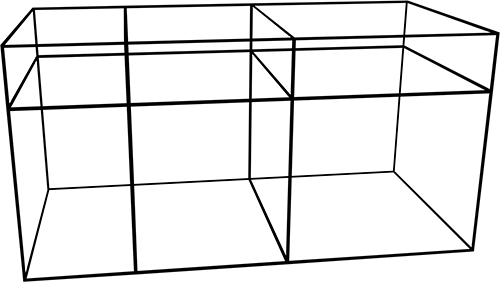
Zur Ermittlung des Schnittpunktes dreier Ebenen kann die Repräsentation der Ebenen in eine Koordinatenform konvertiert werden, und das entstehende Lineare Gleichungssystem mit Hilfe numerischer Methoden gelöst werden. Das Ergebnis stellt dann den Schnittpunkt dar. Die Berechnung erfolgt durch Setzen der Elemente des Normalenvektors als Koeffizienten der Gleichung (Elemente von A) und dem Punktprodukt des Stütz- und des Normalenvektors als Ergebnis b. Wenn man nun jeweils drei Ebenen als drei Kreuz drei Matrix mit Ergebnisvektor betrachtet, kann man das LGS leicht lösen. In diesem Falle fand die eine Funktion der "Eigen" Bibliothek Anwendung. Da das Ergebnis einer Schnittpunkts- Berechnung auch eine Ebene, eine Gerade, oder keinen Schnittpunkt darstellen kann, wurden die drei verwendeten Ebenen zuvor jeweils auf lineare Unabhängigkeit geprüft um Parallelität aus zu schließen.

Eintragen der Kanten

Zwei Knoten sind dann Nachbarn, wenn zwei Ebenen, aus denen sie entstanden sind, gleich sind. Sowohl die Information aus welchen Ebenen sie entstanden sind, als auch welche Nachbarn sie haben, sind in den Eigenschaften der vertecies gespeichert.

Finden der Puzzle-teile

Um alle möglichen Kombinationen für eine Seite des Modells zu finden, müssen alle möglichen Kantenzüge, die diese Seiten beschreiben, berechnet werden. Dies stellt den mit Abstand größten Rechenaufwand dar. Um dabei so effizient wie möglich vor zu gehen, findet eine Implementation Andreas Bayers Anwendung. Diese testet mögliche Puzzle-Teile auf nicht geschlossene Kantenzüge, leere Flächen und zuvor gefundene Ergebnisse.

Die so gefundenen Zyklen werden dann in einer .loops datei gespeichert, um eine erneute Berechnung zu ersparen.

Optimierung

Da die Such nach Zyklen ein NP-vollständiges Problem darstellt, will man die Eingabe Daten natürlich so klein wie möglich halten. Eine hier gewählte Möglichkeit stellt das zusammenlegen von vertecies dar, die an der selben Stelle liegen. Diese entstehen, wenn das Werkstück Flächen hat, die auf einer gemeinsamen Ebene liegen und daher an den selben Stellen mit anderen Ebenen schneiden. Um die Integrität der Nachbarschafts-Beziehungen zu erhalten, wird vorher ein dictionary angelegt, anhand dessen die Zyklen wieder separiert werden können.

Trimmen des Suchbaumes

Um den Suchbaum zu reduzieren, können wir Pfade trimmen von denen wir wissen, dass sie nicht zu legitimen Lösungen führen können. Zu diesem Zweck werden zwei Vektoren gepflegt: in einem werden vertecies gespeichert, die in zukünftigen Iterationen verwendet werden müssen und in dem anderen, welche verwendet werden dürfen (Siehe Fig. 7). Die Grundlage für diese Einordnung ist die Tatsache, dass das fertige Modell wasserdicht sein muss.

Fazit

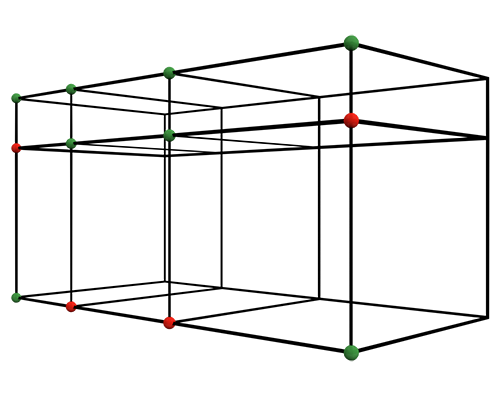
Der Algorithmus funktioniert und liefert korrekte Ergebnisse. Allerdings ist die Auflistung der Zyklen extrem rechenintensiv. Die Berechnung der möglichen Puzzle-Teile aus 13 Knoten dauert schon mehrere Stunden. Weitere Optimierungen sollten daher hier ansetzen.

Mögliche zukünftige Optimierungen

Um die Berechnung unzulässiger vertex-Kombinationen zu vermeiden könnte man sie in den Suchbaum integrieren. Wir können den allowed Vektor verwenden um nur die im nächsten Schritt benötigten, möglichen Puzzle-Teile zu berechnen. Dies erfordert jedoch intelligentes caching, um doppel-Berechnungen zu vermeiden.

Mögliche Fortführung

Das Datenset des Scanners enthält auch Informationen über runde Löcher und abgerundete Ecken. Diese zu implementieren wäre eine Möglichkeit das Projekt fort zu führen.