Now, we present the result of running the algorithms on some created examples. All the created data will have a gray color and we show critical points by red, green, blue and other colors as described in here. We show the results using meshlab and we color a mesh by its vertices, so when a vertex is colored by a specific color,it will affect all the faces containing it.
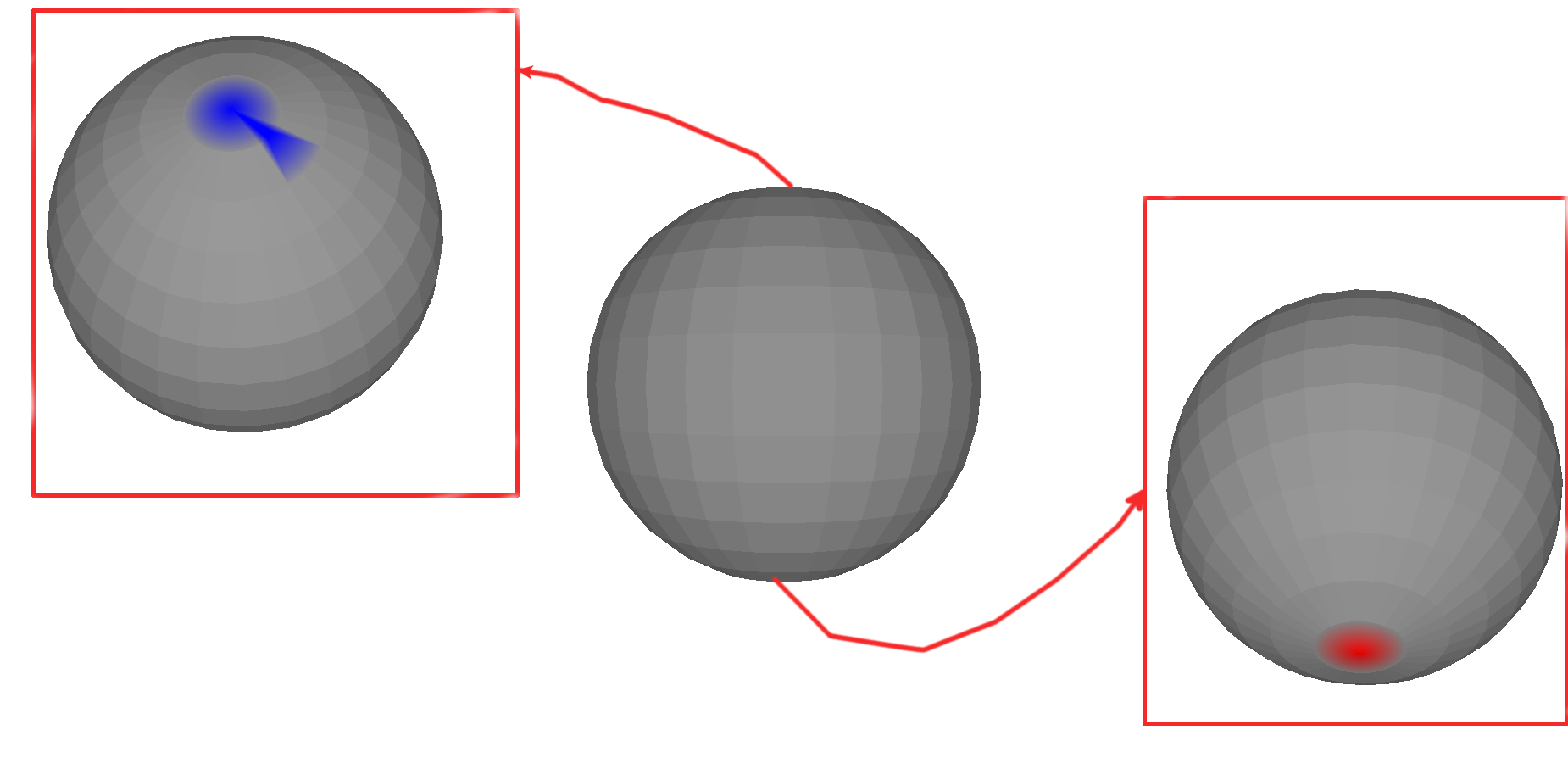
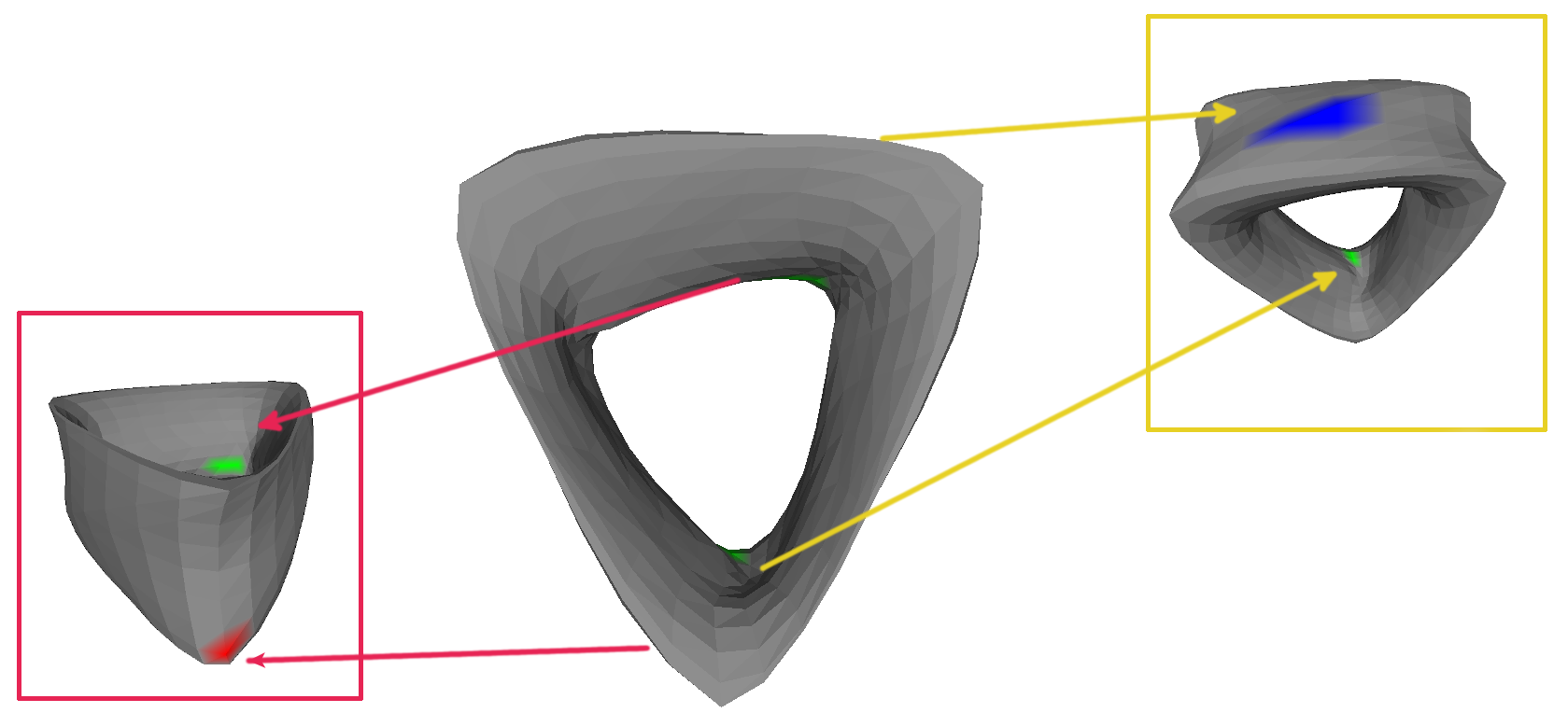
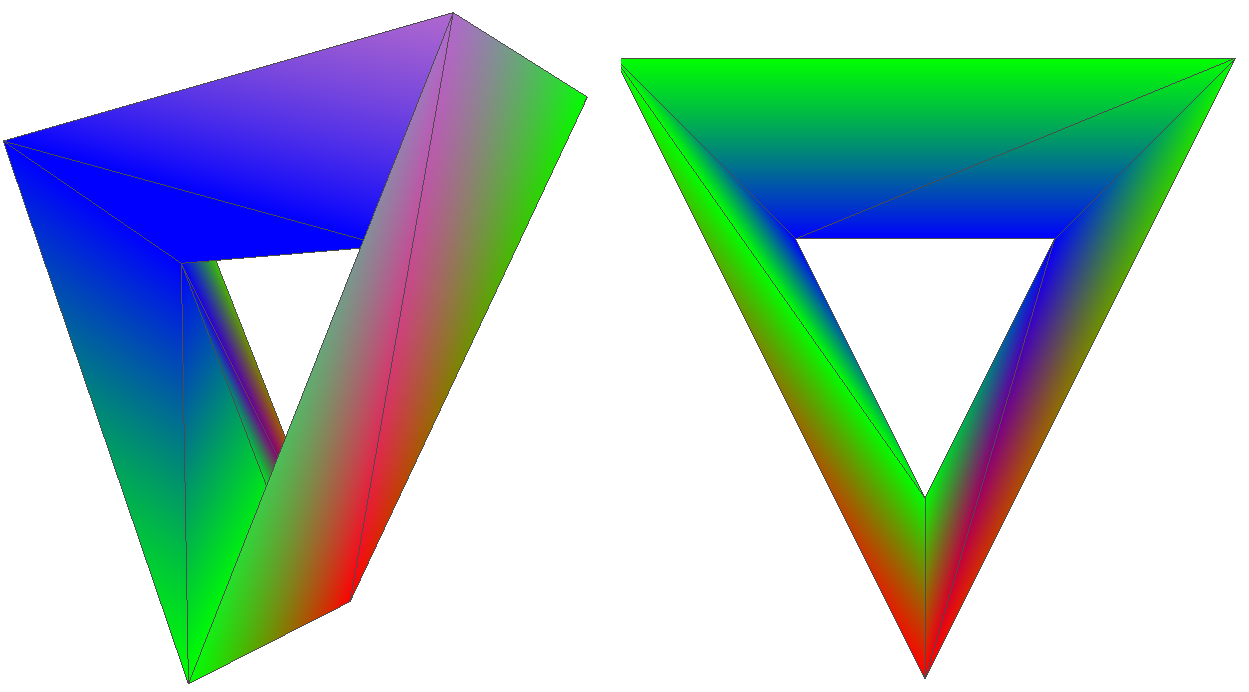First, we test our implementation by running it on known object to find the critical cell. So, we run it first on a simple tetrahedron that consists of 4 vertices and 4 faces. We take the height as a scalar value. Since the tetrahedron homotopy equivalent to the sphere and it has the minimum number of vertices and faces, so we find 2 critical cells on it, namely one point as a minimum (red color) and one triangle as a maximum (blue color). Notice that more than one face has blue or red color, it is because of the color interpolation in the faces as mentioned previously.

Then, We also tested on a sphere with 242 vertices and 480 faces. We take the height as a scalar value. We find two critical cells. A 2-cell on the north pole and 0-cell on the south pole of the sphere.

Then we run the algorithm on torus. First, we begin with the manually calculated example here. The torus in this example has only 9 vertices and 18 faces. We took the height of the torus as an input of the scalar value. So we get one vertex as minimum (red color) and two edges as saddle (green color) and one triangle as maximum (blue color).

Then we test on a torus with 576 vertices and 1152 faces created by Blender.The critical cells are better seen. We have the minimum (red) on the bottom and the maximum (blue) on the top and one saddle (green) on the top of the lower arch and another saddle on top of the higher arch.

Then we create a disturbed torus to make extra minima and maxima. We call this torus the butterfly torus.

When the algorithm run on it, we get one maximum at the top (like the nor- mal torus) and 3 saddles (one more saddle than than the torus in last example) and two minima (also additional)