Model / Algorithm
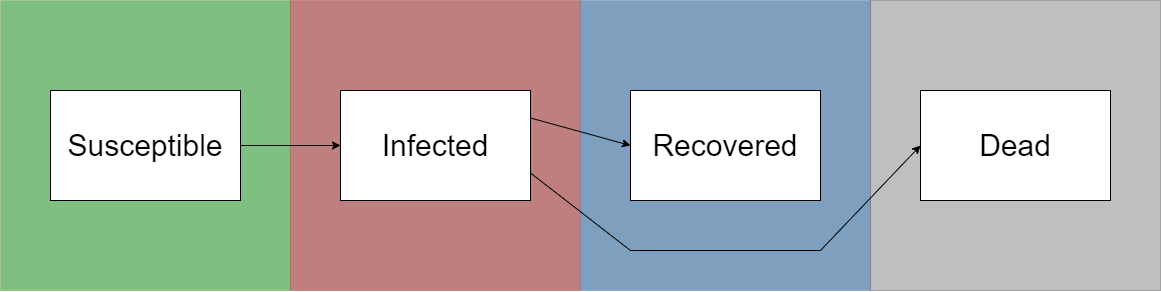
SIRD-Model
- S: Susceptibles, people that have not contracted the virus
- I: Infected, people that have contracted the virus
- R: Recovered, people that have recovered from the virus
- D: Dead, people that have died because of the virus
Gillespie-Algorithm
To realise the simulation a fitting stochastic algorithm is needed. The Gillespie-Algorithm simulates a model in a predefined time interval, e.g. one day, or until a certain state in the model is reached.The model is based on a predefined set of reaction rates and rules. New rules and rates are easily added too. The randomness comes from two randomly generated float-numbers.
Gillespie-Algorithm Steps
- Generate two random floats r1, r2 ∈ [0,1]
- Calculate reaction rates, the total sum and the cumulative sum of the reaction rates
- Advance the time t=t+Δt, Δt is in dependence of r1/TotalRateSum , r1 can be modified by a function, e.g. -log(r1), so that the number of events better fit the desired time frame.
- Divide every value of the cumulative sum by the total sum to place it on the interval [0,1]
- Determine the rule that will be executed with the second float by placing it into the cumulative sum interval
- Execute the rule
- Repeat until time limit is reached or desired model state is reached
Gillespie-Rules for my extended SIRD (excerpt, not all listed)
ι infect rate of the disease, N the sum of people, ρ the recovery rate, δ the death rate, η hospitalisation rate, ω vaccination rate, V available vaccination doses, ϑ testing rate, λ loss of testing rate- I: A susceptible gets infected: S+I → 2I with rate (ι/N)SI
- R: An infected recovers: I → R with rate ρI
- D: An infected dies: I → D with rate δI
- H: An infected gets hosptialised: I0 → I3 with rate η((Bmax-I3)/N)I0
- V: A susceptible gets vaccinated: V + S → V1S with rate ωVS
- T: An unvaccinated susceptible gets tested S0 → S1 with rate ϑS0.
A tested susceptible loses the test status S1 → S0 with rate λS1
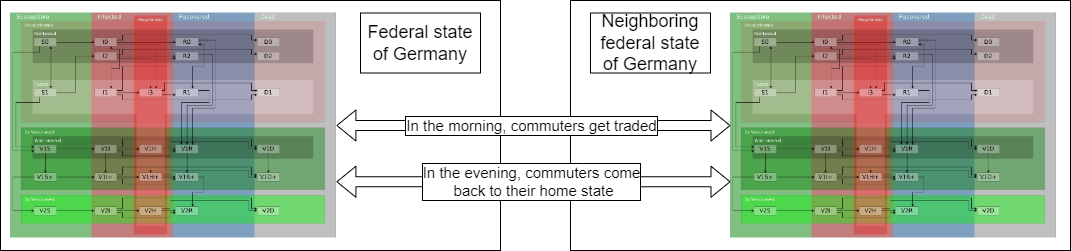
Each federal state of Germany has this model. This enables commuting of people between neighboring states.
Before the first Gillespe-Event takes place, commuters get distributed to the neighboring states. After the
last Gillespe-Event the commuters come home. The commuting individuals get sorted into their respective
category and influence the events happening at the visiting state.
Assumptions made when creating this model
- Once recovered, no reinfection possible
- Every individual is willing to be vaccinated
- Individuals will not be vaccinated while infected
- Individuals in the hospital are always tested
- Positive tested individuals are less likely to infect others than non-tested infected
- Individuals with unknown status change aren't tested again
- Commuters commute before the first Gillespie-event takes place and go back home after the last
- Positive tested individuals don't commute, 1x Vaccinated individuals inside the wait period also don't commute
- Commuters are not able to be hospitalized
- Vaccination of commuters only possible in their own federal state
- Tests are able to determine if a person was already infected
- For each death it gets determined if the cause was the disease or not