Spieler
Autor: Jacob Rose
Bevor ich die Spielerklasse entwickelt habe und richtig mit unserem Projekt loslegte,
experimentierte ich zuerst in 2-d an einem eigenen Projekt um besser
zu verstehen wie die Videospielprogrammierung funktioniert.
Ein großer Unterschied von 2-d auf 3-d, welcher mich in der Entwicklung am meisten Zeit kostetet
war:
Bewegung
Die Bewegung in 2d ist sehr einfach: Der Spieler hat eine Position, bestehend aus x- und y-Koordinaten.
Um ihn zu bewegen führt man Additionen oder Subtraktionen auf die X bzw Y Komponente des Spielers durch,
wenn die Bewegungstasten gedrückt werden.
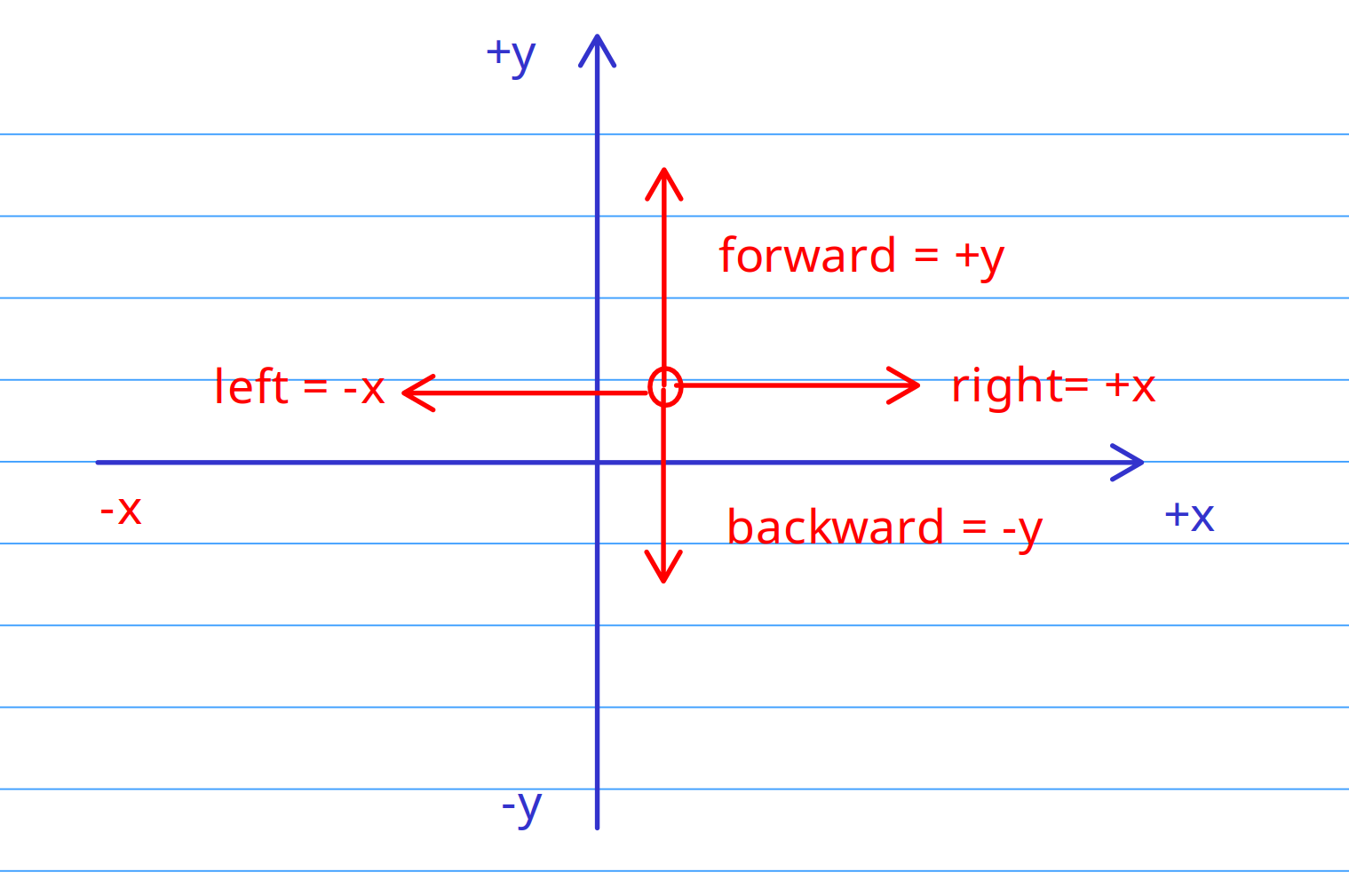
Geht man nun ins 3-dimensionale wird alles komplizierter, da man keine absoluten Werte mehr auf die Position
des Spielers addieren kann. Was links, recht, vorne und hinten ist, hängt nun davon ab wo der Spieler hinschaut.
Die Ausrichtung der Kamera muss also für die Berechnung der Richtungsvektoren mit einbezogen werden.
Für eine Erklärung soll hier zuerst das Koordinatensystem vorgestellt werden. Die Z-Achse zeigt nach
vorne in den Bildschirm hinein, die x-Achse zeigt nach links und die y-Achse
nach oben, so wie in der folgender Graphik:
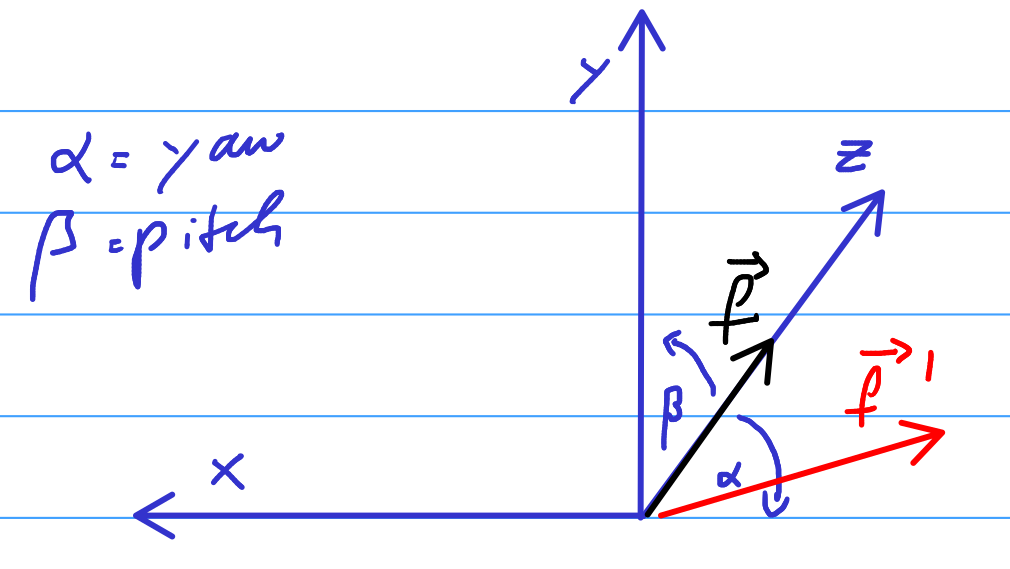
Der Spieler hat im 3-d Raum zwei Freiheitsgrade um der er die Kamera
bewegen kann. Erstens kann er seine Sicht um 90° nach oben und nach unten
verändern. Dies wird durch den Winkel beta, bzw. den Grad an Rotation
um die x-Achse beschrieben. Zweitens kann er sich um 360° Grad drehen.
Diese Drehung um die y-Achse wird beschrieben durch den Winkel alpha.
Für die Bestimmung der Bewegungsvektoren des Spielers reicht es wie im Folgenden
die Werte von alpha mit seinem zugehören Forwärtsvektor in der x/z-Ebene aufzuzeichnen.
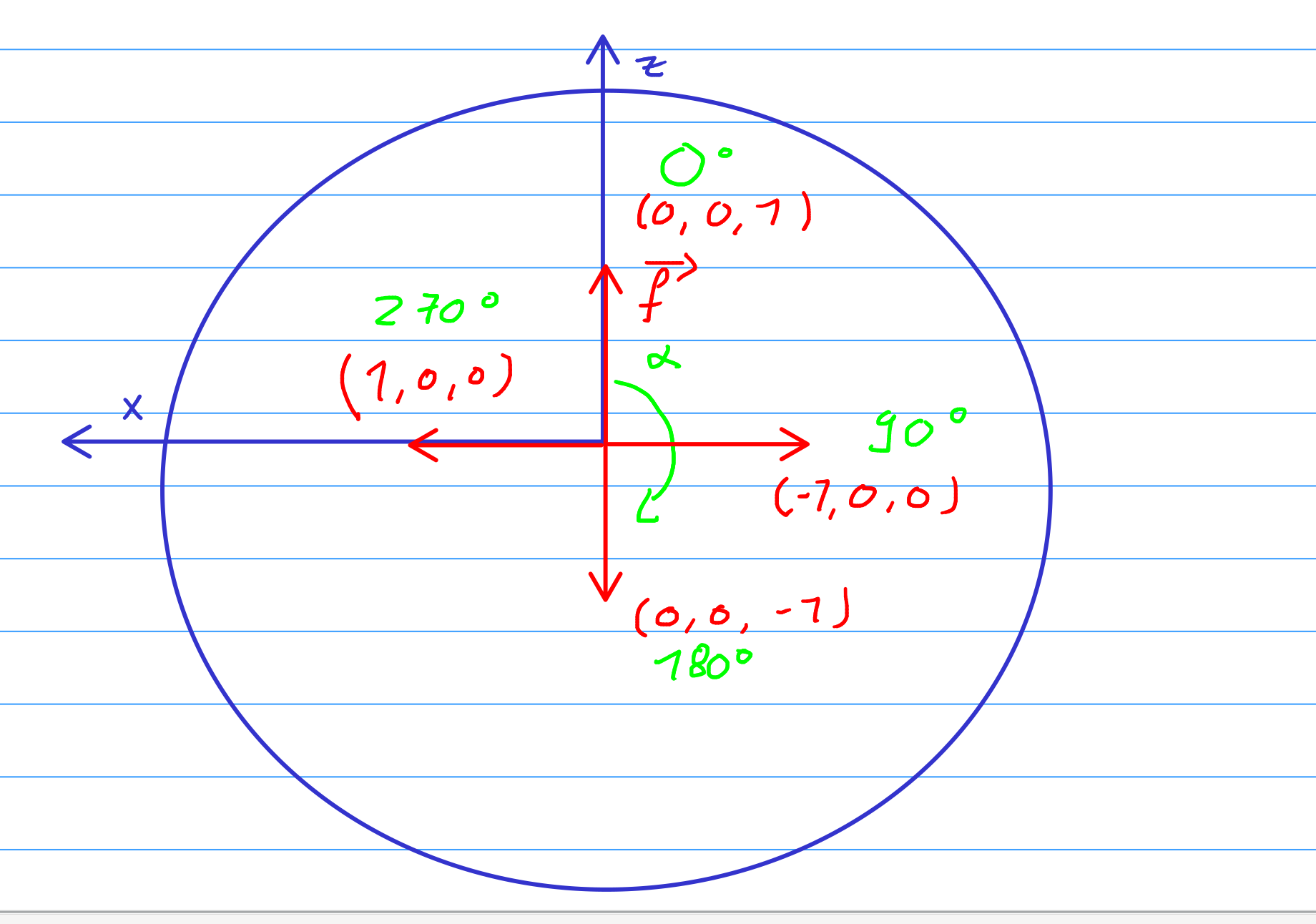
Wenn sich der Spieler nicht dreht, schaut er in richtung (0,0,1),
bei einer Drehung um 90° schaut er in Richtung (-1,0,0) usw.
Trägt man die Werte in eine Tabelle lässt sich leicht die richtige Funktion
für die Bewegungsvektoren ablesen:
|
X |
|
Z |
| alpha |
Result |
alpha |
Result |
| 0 |
0 |
0 |
1 |
| 90 |
-1 |
90 |
0 |
| 180 |
0 |
180 |
-1 |
| 270 |
1 |
270 |
0 |
forward-vector = (-sin(alpha), 0 , cos(alpha))
right-vector = (-cos(alpha), 0 , -sin(alpha))
Bewegungsbereich
Der Spieler kann sich außerdem nicht komplett frei im Raum bewegen.
Im Originalspiel war der Bewegungsbereich des Spielers auf eine Linie
am unteren Bildschirmrand begrenzt. In meiner Umsetzung des Spiels
hat der Spieler einen würfelförmigen Bewegungsbereich, welcher durch eine
selbst-modellierte Barrierentextur gekennzeichnet ist. Diese erscheint wenn
der Spieler den Grenzen zu nahe kommt.


