Stable life forms
A large portion of lifeforms are analgoues of so called still lifes in the GoL - Patterns that start at or quickly reach a stable equilibrium and maintain their shape indefinitely. All of these are shown in the image above. There have been a total of 15 stable shapes identified in 3 dimensions.
It is no surprise that these can usually be spotted by observing no or only minimal change in Betti-numbers. Since the shapes don't visibly change, it suffices to showcase them by providing images, instead of animations, as no significant developement over time occurs.
While stable lifeforms can vary widely in regard to their structural complexity, they all share a very low variance in Betti numbers and tend to have low minimal thresholds necessary to find their persistent features.
The only irrelevant features observed are usually fairly short lived and stem from small fluctuations along their surfaces, due to the nature of their respective kernels. If viewed in detail, one might find 'microscopic' wave-like patterns on the surface.
I additionally computed the variance in Betti numbers over time, using a slight variation of the avergage Betti number over time function shown in the previous section.
This lead to the following observation:
Here we can almost immediately identify all topologically stable lifeforms as having zero (or close to zero) variance in all Betti numbers. Since this is plotted on a log scale, this concerns almost all lifeforms with ID less than 31, where the variance of Betti numbers is primarily due to the lifeform settling into the final shape, though there are exceptions with IDs 3, 8 and 21.
It is noted that one can recognize the original 'morphological classification in the artificial tree of life' to some extend. Consecutive numbers always belong to the same categories, with jumps signifying a switch to another phylogenic group.
The Planomembranomes (IDs 38-41) all have significantly high variance in all Betti numbers, except for ID39, which is stable. The same way the Platonidae family (18-22) all have comparibly higher b0 variance (which is still only ~1), again, with ID18 being stable. Additionally, IDs 19 and 20 belong to rotating bodies only, while in IDs 21 and 22, we see some periodical connecting of internal structures, therefore having more Betti-1 variance.
Contractions and hidden spheres
There are two distinct shapes that exhibit a periodic pulsating behaviour. These are Granome ventilans, as well as Sphaerome ventilans, though the two of them differ significantly in size.
Granome ventilans is visible as the number 31 in the average Betti diagram and has the largest b2 by far. This is mainly due to it forming a multitude of more than 30 small blobs, which are hollow. While it appears as though these spheres momentarily vanish in each pulse cycle, the Cubical Persistence analysis shows that they never completely disappear. They just assume really low values, and are overshadowed by the other co-occuring value jumps within the main sphere.
Each of these blobs contribute to Betti-2, as they are hollow. In each cycle the blobs expand and shrink, which leads some of them to merge momentarily. This merging process is directly visible and quantified by the animated Betti series:
Sphaerome ventilans on the other hand is a much simpler shape, as visible in the following animation:

It is noteable that something is fundamentally different compared to Granome ventilans when looking at the Betti numbers (note that the start point in the video is slightly shifted):
Not visible from the animation alone the Betti numbers show that the inner sphere of Sphaerome ventilans is never fully hollow, therefore it only registers as a variation in b0. Meanwhile the spheres in Granome ventilans register as variations in b2, which shows that they contain true voids.
The most striking thing that one might notice is the apparent nonsensical result of having b0 equaling 0. This would suggest no connected component at all, which clearly contradicts what is visible.
This error is likely due to the shape being connected to itself through the periodic boundary. However, CubicalPersistence automatically disregards the first instance of b0 that survives indefinitely, which normally eliminates the background as being detected as one connected component. However, when the pattern connects with itself, it becomes indetermined what is inside and what is outside our shape.
While we can circumvent this problem by changing the parameters of CubicalPersistence(), it would have the opposite effect for lifeforms where the same issue does not emerge. As the computation of CubicalPersistence() was rather time-intensive and the issue was found only after it ran through all lifeforms, I did not re-run it for these cases yet. One may also keep in mind that b2 being of the unintuitive value 3 might be due to the same reason, as different outside regions can now be detected as voids.
Rotations and internal merging
There are several shapes within the Platonidae family, exhibiting rotational movements around an axis. The simplest of these shape is called Hexahedrome rotans - a large sphere containing 5 visible sphere-like subshapes. While two of them remain stable, the other 3 rotate around the imaginery axis which intersects the stable ones.
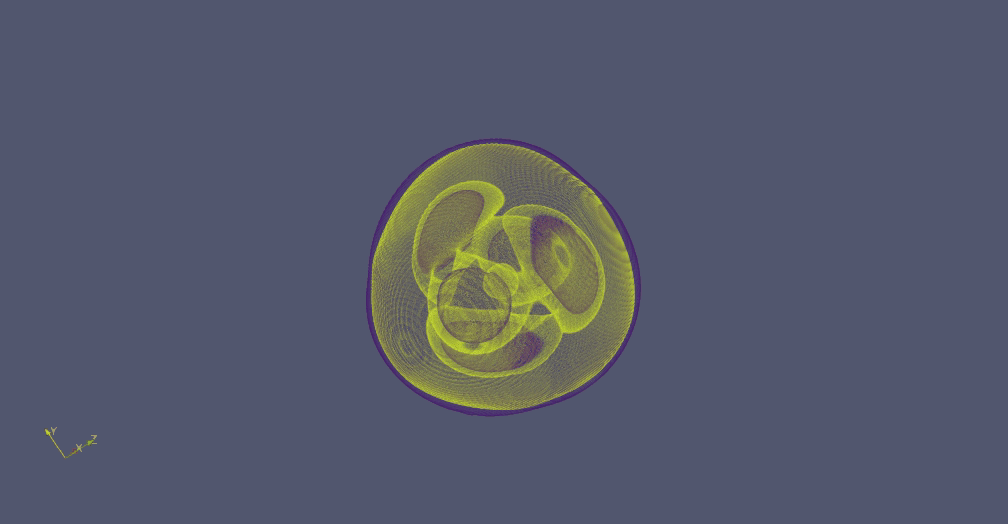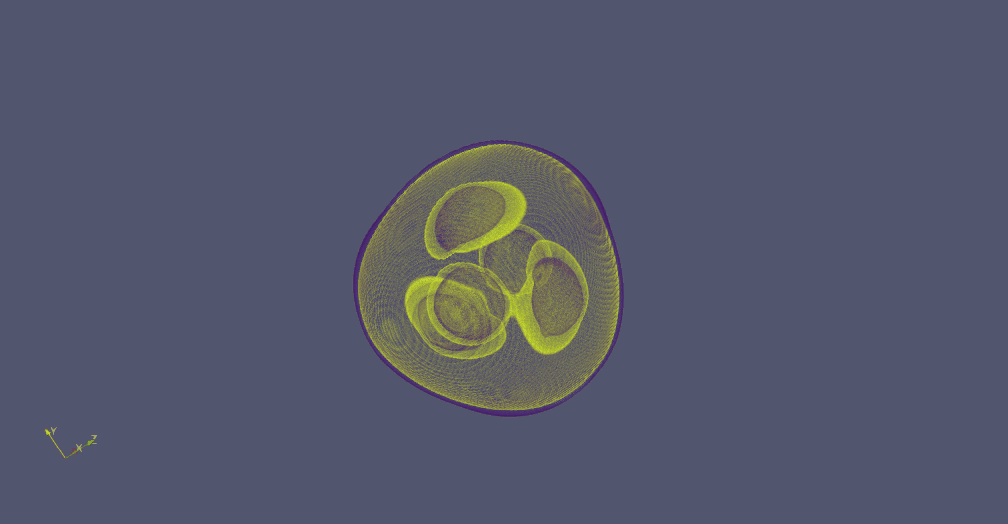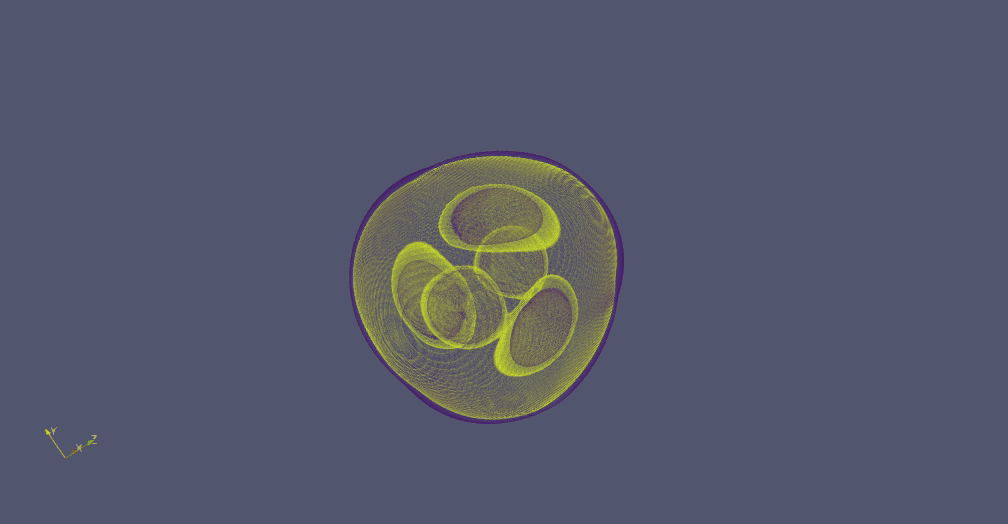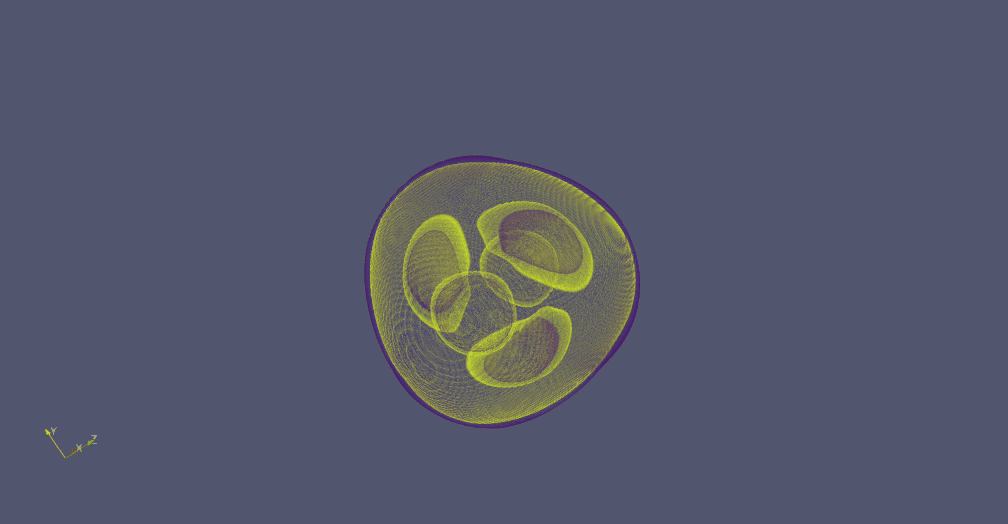 The rotation is fairly slow and it takes the lifeform approximaly 600 frames to complete a full rotation. But since the shape has approximate trilateral symmetry, 200 frames are sufficient to assume the original constellation. Therefore it is an analogue to a 200-oscillator in the GoL.
The Betti numbers show complete stability of topological features, except for the lifeforms initial movement, where the starting pattern has not yet fully settled into the final rotating configuration:
The rotation is fairly slow and it takes the lifeform approximaly 600 frames to complete a full rotation. But since the shape has approximate trilateral symmetry, 200 frames are sufficient to assume the original constellation. Therefore it is an analogue to a 200-oscillator in the GoL.
The Betti numbers show complete stability of topological features, except for the lifeforms initial movement, where the starting pattern has not yet fully settled into the final rotating configuration:
In this case there are 5 separate connected components and 3 voids. This is not intuitive given the visualization, where one would expect either 0 or 5 voids and 6 connected components. This is accounted for by the same mechanism as described with Sphaerome ventilans. Accounting for the issues arising due to the periodic boundary conditions, we arrive at exactly 6 connected components as expected.
Further study shows that this exact issue consists for all spherical lifeforms which barely touch the boundary, which is why we can assign the same correction.
The other simple example is Tetrahedrome rotans, which has tetrahedronal symmetry.
Among the rotational bodies are two special cases. These are Octahedrome torquens and Hexahedrome inversus.
Let's take a look at Hexahedrome inversus first:
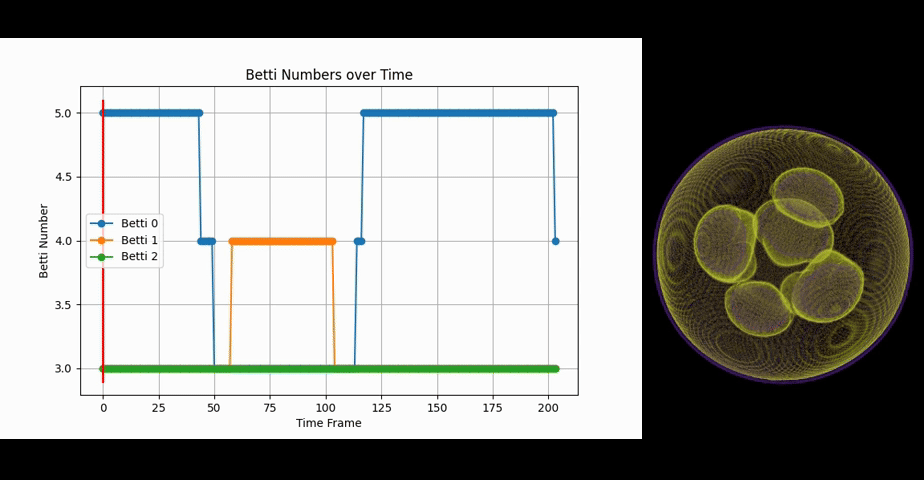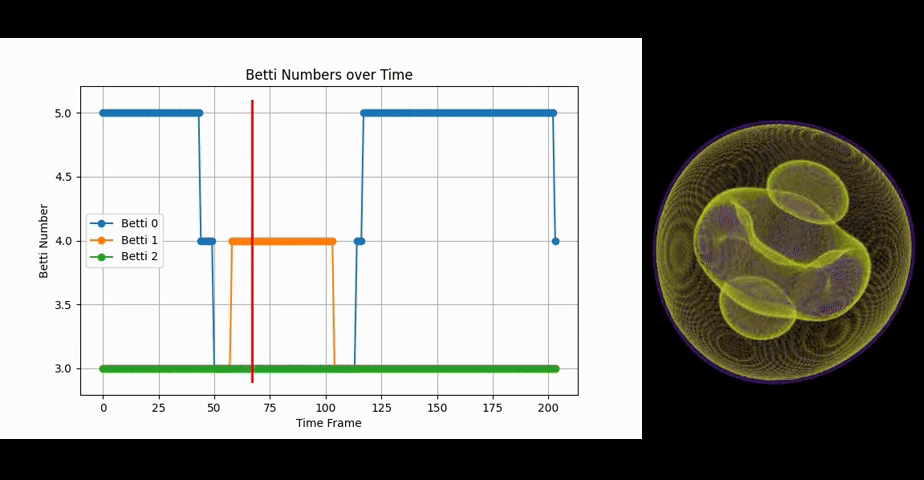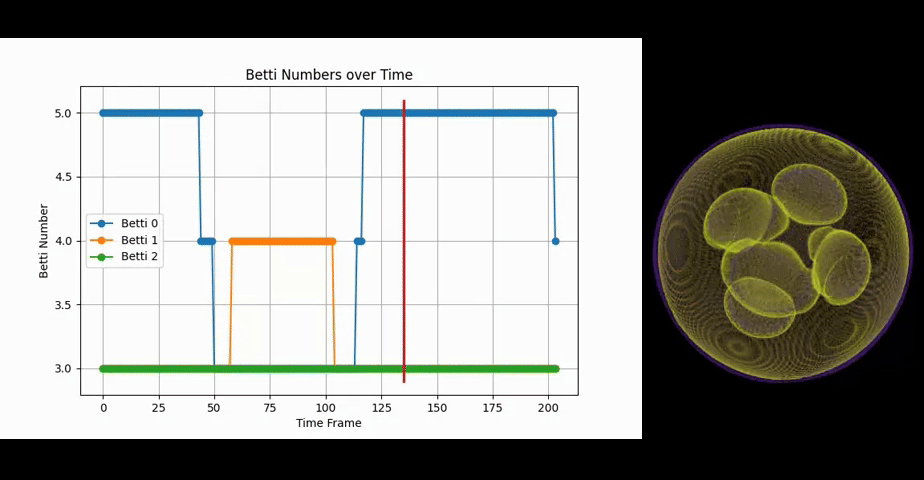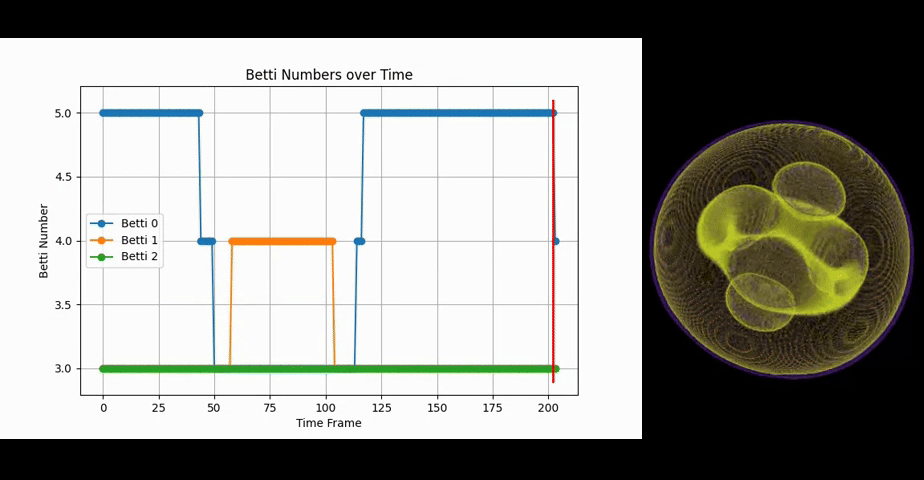
We notice that it starts in a practically identical configuration to the previous example. But instead of rotating, we have three spheres merging periodically. In this case this is represented by the reduction of the connected components by two, as the spheres become a single torus momentarily. The lifeform also increases Betti-1 during the merging. But the change in Betti-1 occurs only after the change of Betti-0 has already taken place and reverses before Betti-0 goes back to the original value. This represents the 'surface' of the 3 spheres connecting first before the whole interior of them has also fully connected, forming a topological torus. One can get an intuition for this by observing how the violet interior connects while the Betti-1 change takes place. The violet volume here represents fairly low but nonzero values.
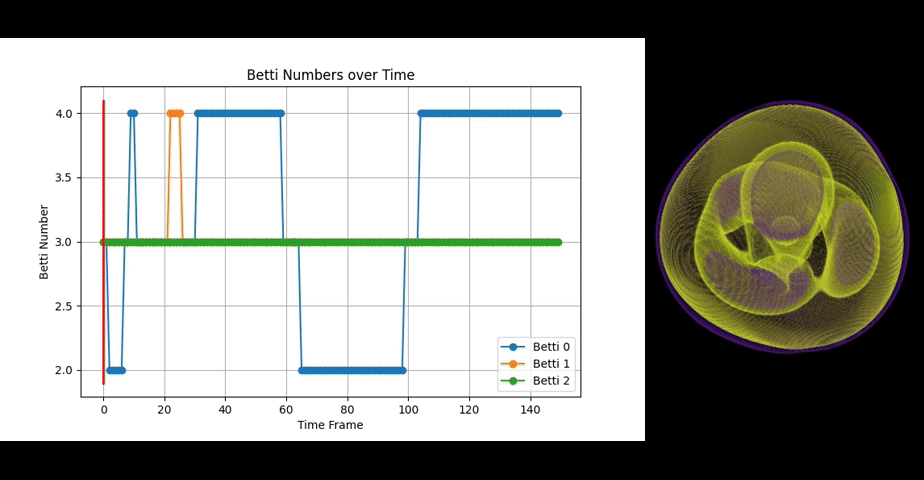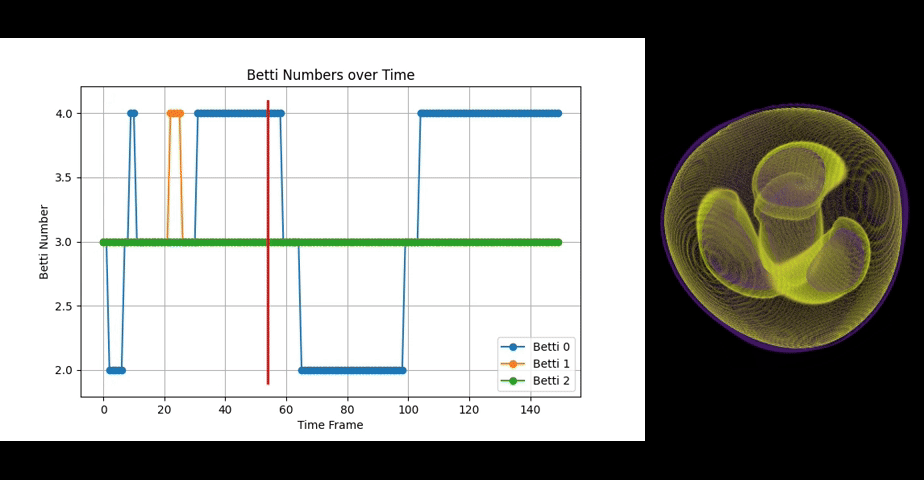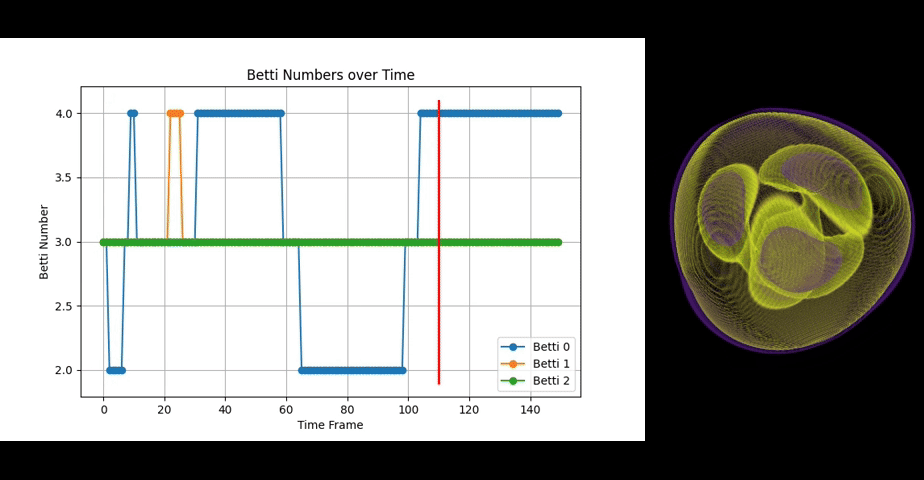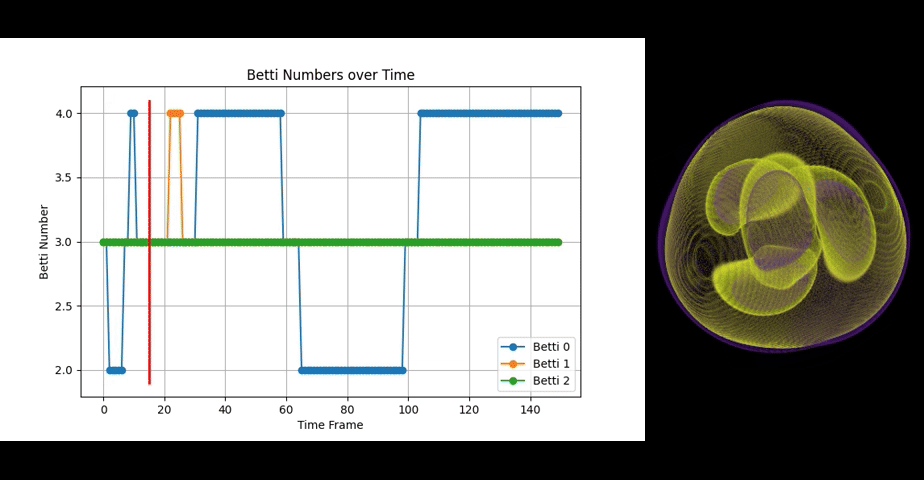
Octahedrome torquens showcases fluctuations in Betti numbers primarily due to the 4 rotating spheres regularly touching and partly merging during those touches.