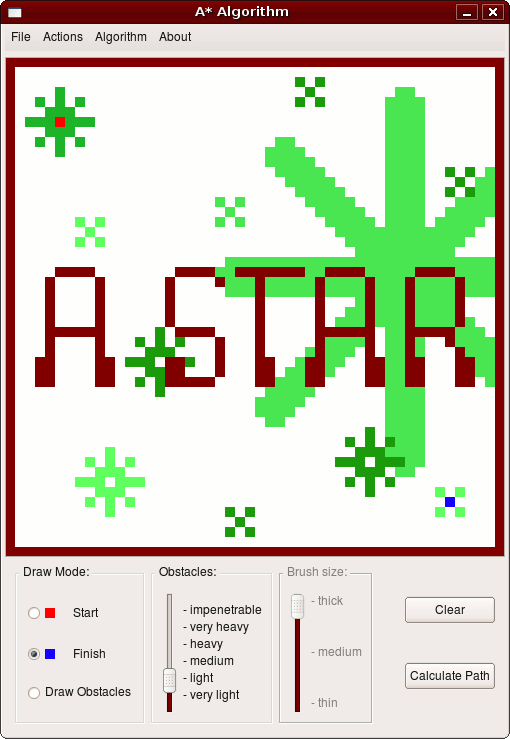
Es sollte ein Programm geschrieben werden, welches den günstigsten Weg zwischen einem Start- und einem Zielpunkt (um Hindernisse herumführend) mit dem A*-Algorithmus berechnet, und sowohl die Punkte als auch den Weg graphisch ausgibt.
Einarbeitung in Qt zum GUI-Design
Freies Wählen eines Start- und Zielpunktes auf einem regulären Gitter
Das freie Setzen von Hindernissen soll möglich sein
Erstellte Szenen sollen abgespeichert werden können
Berechnung des optimalen Pfades über den A*-Algorithmus
Visuelle Darstellung des optimalen Pfades
Optimale Wegsuche bei unterschiedlich gewichteten Pfaden, zum Beispiel in Computerspielen: Berücksichtigung des Blickwinkels von Spieler und Gegner, „Schleichen und Eilen“.
Der A*-Algorithmus ist ein informierter Suchalgorithmus. Er berechnet den kürzesten Pfad zwischen zwei Knoten eines Graphen.
Er findet immer die optimale Lösung, falls eine Lösung existiert.
Erstmals wurde er 1968 von Peter Hardt, Nils Nilsson und Bertram Raphael beschrieben.
Routenplaner
Computerspiele



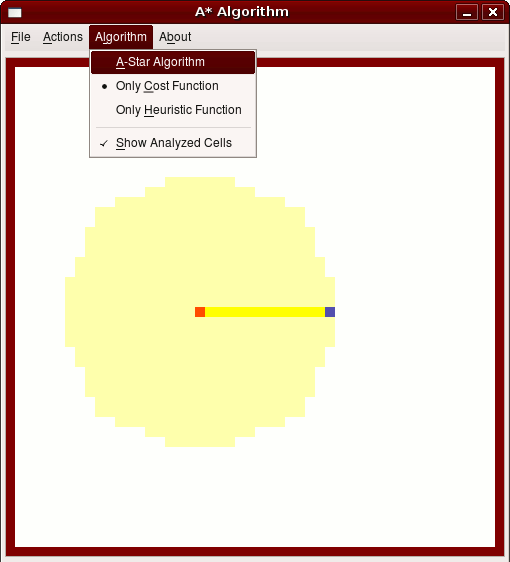
Der Dijkstra-Algorithmus (Abb. 1 links) nutzt keine Information über die Position des Zielpunktes bei der Suche. Er sucht gleichmäßig in alle Richtungen bis er das Ziel findet. Die dabei untersuchten Knoten sind hier gelblich unterlegt, der gefundene Pfad gelb markiert.
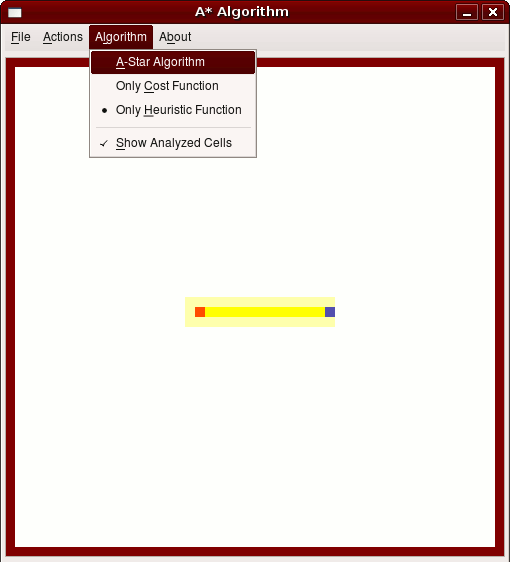
Mit weit weniger untersuchten Knoten kommt ein Algorithmus basierend auf einer Distanz-Schätzfunktion (Abb. 1 rechts) aus. Er muss aber über die Position des Zielpunktes informiert sein.
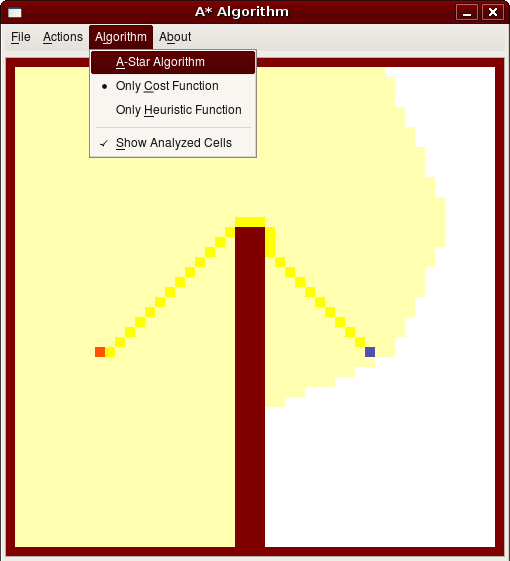
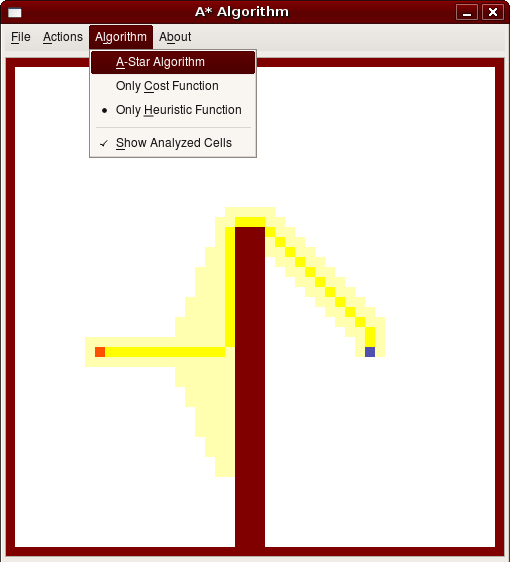
Allerdings liefert der Algorithmus auf Basis der Schätzfunktion im Normalfall keine optimale Lösung, Dijkstra hingegen schon, wie man am nachfolgenden Beispiel sehen kann:
Der
A*-Algorithmus liefert wie der Dijkstra-Algorithmus eine optimale
Lösung, muss dazu aber im Durchschnitt weniger Knoten untersuchen. Im
besten Falle sind dies genau so viele Knoten, wie der Algorithmus
nur über die Schätzfunktion untersucht. Dieser Fall tritt dann auf, wenn kein Hindernis auf der direkten
Verbindungsstrecke zwischen Start- und Zielpunkt liegt. Im
schlechtesten Fall sind dies ebenso viele, wie der Dijkstra-Algorithmus
analysieren muss, zum Beispiel in einem Labyrinth.
Die drei Knotenkategorien:
unbekannte Knoten:
wurden
noch nicht untersucht, sind deshalb noch in keiner Liste
gespeichert, bleiben entweder unbekannt oder werden zu bekannten Knoten.
bekannte Knoten:
wurden vom Algorithmus untersucht und auf die Open List (= Liste der bekannten Knoten) gesetzt. Zu diesen Knoten ist mindestens ein Weg zum Startpunkt bekannt.
abschließend untersuchte Knoten:
wurden als kostengünstigste Knoten ausgewählt, von der Open List gelöscht und auf die Closed List gesetzt. Zu diesen Knoten ist ein optimaler Weg zum Zielpunkt bekannt.
Vorgehensweise des Algorithmus
1. Schreibe alle Nachbarzellen der aktuellen Zelle mit ihrem Wert und einem Zeiger auf die aktuelle Zelle in die Open List. (Aktualisieren oder überspringen, falls nötig)
2. Sortiere die Open List. Zelle mit kleinstem Wert wird zu aktueller Zelle, in die Closed List eingetragen (mit Vorgängerzeiger) und aus der Open List gelöscht.
3. Wiederhole 1. und 2. bis Zielzelle als Nachbarzelle gefunden.
4. Erstelle Pfad = gebe relevanten Teil von der Closed List rückwärts aus (folge den Vorgängerzeigern)
Speichern und Laden von Szenen:
Für diese Funktionalität wurde ein simples eigenes ASCII-Dateiformat
entwickelt (.AST), das den Startpunkt, den Zielpunkt, leere Felder und die
Hindernisse als einfache Zahlenwerte speichert.
6 verschiedene Hindernisstärken:
Neben undurchdringbaren "Mauern" lassen sich auch "Sandgruben",
d.h. begehbare Felder mit höheren Kosten als Hindernisse setzen.
3 verschiedene „Pinselgrößen“:
Erleichtert das Zeichnen von Hindernissen.
3 verschiedene Algorithmen wählbar
Für die Open List wurde der Datentyp Vector aus der Standard Template Library (STL) verwendet. Diese Art von Array bietet den Vorteil, während der Laufzeit dynamisch erweiterbar zu sein. Innerhalb des Vektors bestehen die Elemente aus dem selbstdefinierten abstrakten Datentyp cell, in dem folgende Werte gespeichert werden:
Kosten aus Kostenfunktion g
Kosten aus Kostenfunktion h
Gesamtkosten f = g + h
Zeiger auf vorherige Zelle
Position der Zelle in 2D-Koordinaten (QPoint).
Da in jedem Iterationsschritt fünf neue Zellen analysiert werden müssen und die jeweils nächstgünstigste Zelle ausgewählt werden muss, bietet sich eine Sortierung der Open List hinsichtlich der Gesamtkosten an.
Um die Sortierung möglichst effizient zu gestalten, wurde sie als eine Prioritätswarteschlange über einen binären Heap implementiert.
Ein binärer Heap ist eine Datenstruktur in Form eines Binärbaums, für den folgende Bedingungen gelten müssen:
alle Schichten, bis auf die letzte, müssen vollständig aufgefüllt sein
die letzte Schicht muss linksbündig aufgefüllt sein => balancierter Baum
die Heap-Bedingung muss erfüllt sein:
z.B. Min-Heap: der Schlüssel jedes Kindes eines Knotens muss größer-gleich dem Schlüssel des Knotens selbst sein
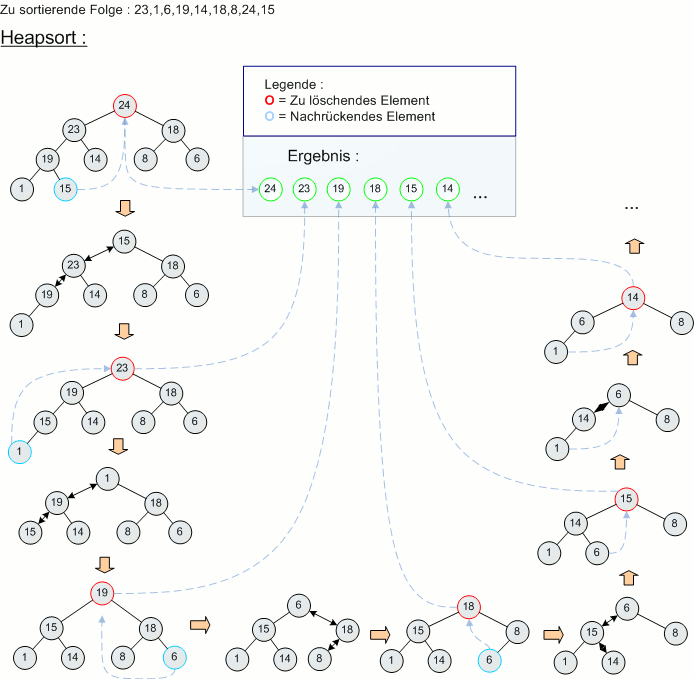
Im average case sortiert ein binärer Heap ein Array mit zufällig angeordneten Zahlen mit einer Komplexität von O(n*log(n)).
Ein binärer Heap und der Heapsort-Algorithmus ist bereits in der STL integriert und kann direkt auf einen STL-Vector angewandt werden. Die einzig notwendige Anpassung ist die Definition eines Sortierkriteriums, wobei in unserem Fall absteigend nach den Gesamtkosten f sortiert wurde. Da die Gesamtkosten während der Laufzeit monoton fallen und bei einem dynamischen Array das Einfügen weiterer Elemente an der Anfangsposition zu rechenzeitaufwändig ist (da alle folgenden Elemente verschoben werden müssen), wurde die Open List in umgekehrter Reihenfolge gespeichert. Hier steht also das kostengünstigste Element an letzter Stelle. Dies hat auch den Vorteil, dass während des Identifizierens der neuen Nachbarn nur unter den letzten sechs Elementen nach bereits besuchten Knoten gesucht werden muss.
Die Closed List wurde ebenfalls als STL-Vector implementiert. Sie wird erst nach der vollständigen Erstellung der Open List mit Werten gefüllt. Da innerhalb des Datentyps cell jeweils ein Zeiger auf die Vorgängerzelle gespeichert wird, welche, ausgehend vom Zielpunkt, durch die Heap-Sortierung auch die kostengünstigste Zelle ist, kann man so sehr leicht den günstigsten Weg vom Zielpunkt zum Startpunkt zurückverfolgen. Wenn man sich die Open List als Binärbaum vorstellt, entspricht das dem dem Verfolgen des insgesamt kostengünstigsten Asts vom Blatt (Ziel) bis zur Wurzel hin (Start).
Die heuristische Funktion schätzt die Kosten des Weges von einer Zelle zum Zielknoten. An sie wird die Anforderung gestellt, dass diese niemals die tatsächlichen Kosten überschätzen darf. Unter dieser Bedingung würde schon der euklidische Abstand als Schätzfunktion ausreichen (bei minimalen Knotengewichten >=1). Da unsere Anwendung allerdings auf einem regulären Gitter arbeitet, konnten wir die heuristische Funktion strenger formulieren:
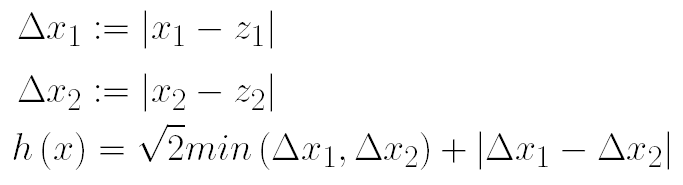
Das Kantengewicht zwischen zwei direkt benachbarten Felden wird mit 1 abgeschätzt, das Gewicht zwischen diagonal benachbarten Feldern, entsprechend des euklidischen Abstands zweier Einheitszellen, mit sqrt(2).

n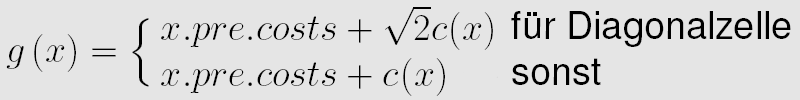
Die Kostenfunktion g speichert, ausgehend vom Startpunkt, die Kosten des bisher gelaufenen Wegs. Dabei werden einfach die Kosten von der Vorgängerzelle mit den aktuellen Kosten c(x) addiert. c(x) ist abhängig von der Gewichtung der Zellen, die durch eventuell vorhandene Hindernisse definiert wird: Für Felder ohne Hindernisse wurde sie auf den Wert 1 gesetzt, für Felder mit begehbaren Hindernissen entsprechend der Hindernisstärke auf 1.8, 3.0, 4.0, 5.0 oder 6.0. Undurchdringbare Hindernisse wurden mit den Kosten 9999 bewertet. Die Stärke der Hindernisse ließe sich auch beliebig anders wählen, diese Werte haben sich aber in unseren Testläufen als praktikabel erwiesen.
In Diagonalrichtung werden die Zellen zusätzlich noch mit dem Faktor sqrt(2) gewichtet, der dem euklidischen Abstand diagonal benachbarter Einheitszellen entspricht.

