TerrainViewer
Die in C++ programmierte Konsolenanwendung "TerrainViewer" verwendet zur dreidimensionalen Darstellung digitaler Geländedaten die Graphikbibliothek OpenGL. Die GUI wurde mit Hilfe von GLUI implementiert, welche fester Bestandteil des Utility Toolkits GLUT ist. Zum Einlesen von Texturen, wird die Bibliothek SDL verwendet. Alle Bibliotheken und somit auch der TerrainViewer sind plattformunabhängig.
Den Sourcecode habe ich ich in der Entwicklungsumgebung Eclipse geschrieben und mit Hilfe von Cygwin kompiliert. Das Programm durchlief bis zur Fertigstellung insgesamt vier Phasen.
Phase 1: Einlesen und Darstellung digitaler Geländemodelle
In der ersten Entwicklungsphase kümmerte ich mich darum ein digitales Geländemodell einzulesen und zunächst auf irgendeine Art und Weise darzustellen. Als Quelle diente dazu ein DGM im Arc/Info ASCII Grid Format, da dieses auch ohne spezielle Bibliotheken leicht eingelesen werden kann.
Einlesen von ARC/Info ASCII Grids
Zunächst wird dazu ein M x N Array bestehend aus Integer Zahlen erstellt und dann Wert für Wert aus dem Datengitter (bestehend aus M Zeilen und N Spalten) ausgelesen und in das Array gespeichert. Das Array ist als Speicher besser geeignet als eine verkette Liste, da später beim Zeichnen mit Indizes schneller auf die einzelnen Werte zugegriffen werden kann.
3D Darstellung der Daten
Nachdem das Einlesen korrekt funktionierte, wandte ich mich dem schwierigeren Teil zu, nämlich der Darstellung der Daten aus diesem Array. Zum Zeichnen verwende ich folgendes Verfahren:
- Initialisierend wird ein Quadrat erstellt, dessen Eckpunkte den "Eckpunkten" des Arrays entsprechen ([0][0], [0][N], [M][0], [M][N])
- Dieses Quadrat wird dann rekursiv in jeweils vier Quadrate unterteilt, bis die gewünschte Detailstufe erreicht ist. Mit diesem Verfahren können alle Punkte im Gitter bzw. im Daten-Array erreicht werden.
- Nachdem die gewünschte Detailstufe erreicht ist, werden alle Quadrate jeweils in zwei Dreiecke unterteilt, welche sich die Diagonale des Quadrats als Hypotenuse teilen.
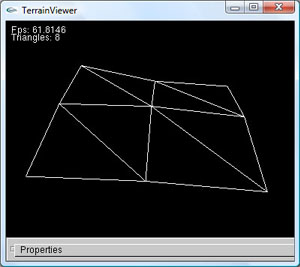
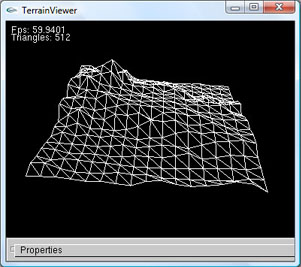
Da es sich bei dem Zeichenalgorithmus genau genommen um eine Unterteilung in spezielle Rechtecke (Quadrate) handelt, funktioniert dieser theoretisch auch mit nicht quadratischen Geländedaten. Mit Steigender Abweichung der Zeilenanzahl zu der Spaltenanzahl würde jedoch die Qualität des Ergebnisses sinken.
Phase 2: Farbe, Textur und Licht
An dem weißen Gittermodell kann man bereits Geländeformen und Strukturen erkennen. Ab einer bestimmten Detailstufe oder der Darstellung des Geländes mit ausgefüllten Dreiecken sieht man jedoch nicht mehr als ein weißes Quadrat. Das digitale Geländemodell selbst kommt jedoch ohne jegliche Oberflächeninformation. Es gibt dennoch zwei Möglichkeiten Oberflächeninformation über andere Quellen zu erhalten oder künstlich auf Basis des digitalen Geländemodells zu erzeugen und darzustellen.
Höhenabhängige Geländefärbung
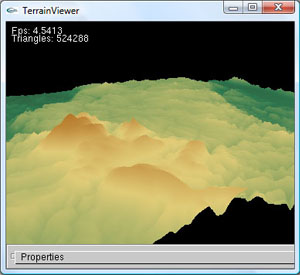

Die eine Möglichkeit ist jedes Dreieck unterschiedlich zu färben, wobei die Farbe in Abhängigkeit von der Höhe der Punkte, welche das Dreieck aufspannen, bestimmt wird. Zunächst werden für alle sinnvollen Höhenbereiche repräsentative Farben gewählt und die Farben innerhalb eines Höhenbereichs zwischen den beiden angrenzenden Farben interpoliert. Die Farben der verschiedenen Höhenbereiche werden so gewählt, dass sie der natürlichen Farbgebung in diesem Bereichen am ehesten entsprechen. Für den Höhenbereich zwischen 0 und 500 Meter wird z.B. die Farbe Grün (Bäume), oberhalb von 1000 Meter die Farbe Gelb (Sträucher) und oberhalb von 3000 Meter die Farbe Weiß (Schnee) gewählt. Zwischen den Eckpunkten der Dreiecke werden die Farben nochmals mittels Gouraud-Shading interpoliert um weiche Übergänge zu erhalten.
Es werde Licht
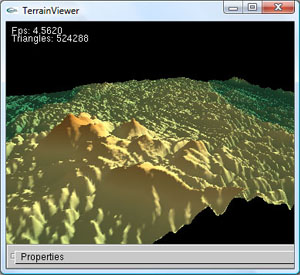

Die Struktur des Geländes ist nun auch bei ausgefüllten Dreiecken klar erkennbar. Insgesamt wirkt das Ergebnis aber noch sehr unrealistisch, da es mehr einer gefärbten Wolke als einer Landschaft ähnelt. Seitlich einfallendes Licht z.B. lässt die Szene realistischer wirken. Damit das Licht korrekt reflektiert wird, wird für jedes Dreieck die zugehörige Normale mit angegeben. Die Berechnung dieser Normalen geschieht vor dem Zeichnen für alle Gitterpunkt. So bleibt der Zeichenroutine permanenter Rechenaufwand erspart, da die Normalen nur einmal bei der Initialisierung und nicht bei jedem Neuzeichnen berechnet werden müssen. Um eine Facettierung zu verhindern und auch bei einer groben Gitterstruktur eine weiche ineinander übergehende Landschaft zu erhalten wird Phong-Shading verwendet. Es wird also nicht nur für jedes Dreieck eine Normale angegeben, sondern für jeden Eckpunkt eines jeden Dreiecks. Beim Zeichnen werden dann zusätzlich alle Normalen innerhalb der jeweiligen Dreiecke zwischen den gegebenen Normalen interpoliert. Da die Normalen auf dem feinsten Gitter berechnet wurden, erzeugt dies auf einem gröberen Gitter jedoch sogenanntes – und in diesem Fall unerwünschtes – Bumpmapping. Auch wenn bei der höchsten Detailstufe ein sehr schönes Ergebnis erzielt werden kann, ist dieses Verfahren für mein eigentliches Ziel die Dreiecke zu reduzieren daher ungeeignet.
Textur
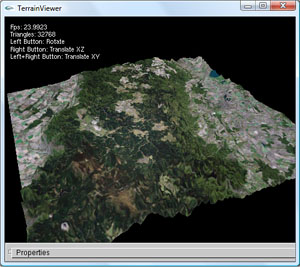
Oberflächeninformation lassen sich auch in Form einer Textur über das Dreiecksgitter legen. Da die Farben bei diesem Verfahren unabhängig von dem digitalen Geländemodell bestimmt werden, kann die Textur auch bei reduzierten Dreiecksgittern verwendet werden ohne Qualitätsunterschiede zu erkennen. Legt man beispielsweise Satellitenbilder als Textur über das Gelände, wirkt das Gelände noch realistischer. Die TerrainViewer Applikation kann Texturen im verlustfreien Bitmap-Format mit Hilfe der SDL Bibliothek einlesen. Damit das Einlesen der Textur korrekt funktioniert, muss für Ihr Format gelten: Breite = Höhe = 2n Pixel. (Auf Nvidia-Graphikkarten funktionieren auch andere Formate)
Phase 3: Dreiecksreduzierung
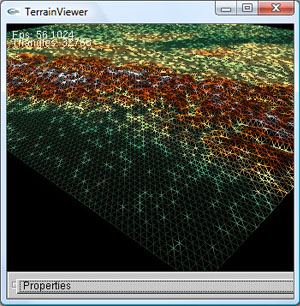
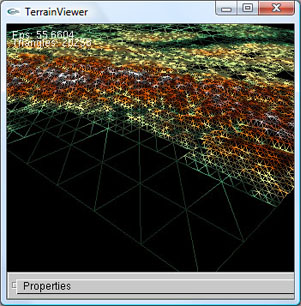
Die SRTM Daten kommen in 1° Paketen, welche aus insgesamt 6000 ⋅ 6000 = 36 Mio. Gitterpunkten bestehen. In der Terrainviewer Applikation entspricht dies bei der feinsten Detailstufe 2 ⋅ (Zeilen - 1) ⋅ (Spalten - 1) ≈ 72 Mio. Dreiecken. Diese Zahlen schaffen einen Eindruck, in welchen Größenordnungen wir uns bewegen. Um das Gelände in Echtzeit zu rendern, ist ein Verfahren notwendig, welches die Dreiecke enorm reduziert und nach Möglichkeit die Qualität des Geländes nicht sichtbar vermindert. Erreicht werden kann dies, indem das Gelände nur an nötigen Stellen verfeinert wird ("Level of Detail"). Planare Geländebereiche wie z.B. ein Fussballplatz können nämlich im Vergleich zu rauen Geländebereichen wie z.B. einem Berg mit weniger Dreiecken dargestellt werden ohne einen qualitativen Unterschied erkennen zu können. Verfeinert wird also nur, wenn die Differenz zwischen dem linear interpolierten y-Wert entlang der Diagonalen des Quadrats und dem realen y-Werte einen bestimmten Wert übersteigt. Der folgende Pseudocode soll das Verfahren verdeutlichen:
Pseudocode:
/* <<< Initialisiere temp_quadrat_liste mit einem Quadrat */
while (detail_stufe <= hoechste_detail_stufe)
{
quadrat_liste = temp_quadrat_liste;
while (quadrat_liste)
{
if (Interpolationsfehler(quadrat) > max_fehler)
{
/* <<< Interpolationsfehler ist zu gross. Teile daher
* <<< Quadrat in 4 Quadrate auf und hänge diese
* <<< an die Liste temp_quadrat_liste an */
}
else
{
/* <<< Interpolationsfehler liegt im akzeptablen Bereich.
* <<< Hänge daher das Quadrat unverändert an Liste
* <<< temp_quadrat_liste an */
}
detailstufe++;
}
}
Der Algorithmus arbeitet nach dem Top-Down Prinzip. Bei ungünstig geformten Geländen können dadurch Interpretationsfehler auftreten. Um diese Interpretationsfehler zu vermeiden, wird nicht nur der Mittelpunkt sondern jeder Punkt auf der Diagonalen eines jeden Quadrats überprüft. Dadurch steigt zwar der Rechenaufwand, aber inakzeptable Fehler werden vermieden. Schöner wäre natürlich ein Algorithmus, welcher nach dem Bottom-Up Prinzip arbeitet, dieser wäre aber weitaus schwieriger zu implementieren.
Ergebnis:- Das Verfeinerungskriterium reduziert die Dreiecke abhängig vom Gelände und den Einstellungen um durchschnittlich 50-100%.
- Zwischen Quadraten unterschiedlicher Detailstufe, entstehen unschöne Lücken (sogenannte "Cracks"), wenn der angrenzende y-Wert der detaillierten Quadrate vom gröberen Quadrat abweicht.
Phase 4: Kamerasteuerung
In der letzten Phase war es mein Ziel eine vernünftige und intuitive Kamerasteuerung zu implementieren. Die Kamera sollte dabei aus der Vogelsperspektive auf das Gelände blicken und die Position sowie Blickwinkel mit möglicht wenigen Transformationen geändert werden können. Da OpenGL lediglich eine Funktion (gluLookAt(...)) zur Angabe von Kameraposition und Blickpunkt anbietet, musste ich die Funktion zur Transformation selbst implementieren.
Kugelkoordinaten
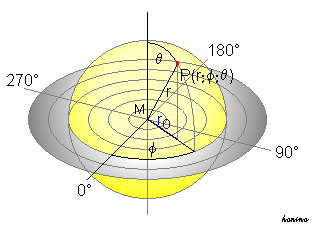
Damit der Blickwinkel der Kamera geändert und die Kamera an beliebige Positionen transformiert werden kann, ist die Berechnung von sogenannten Kugelkoordinaten notwendig. Die Position der Kamera und die Blickrichtung werden bei jeder Änderung an die Funktion gluLookAt() übergeben. Die Berechnung der Kameraposition und dem Blickpunkt basiert dabei auf folgendem Prinzip:
Die Position der Kamera befindet sich in der Mitte M einer Kugel mit dem Radius r = 1. Der Blickpunkt P bewegt sich auf der Kugeloberfläche und hat daher stets den gleichen Abstand zur Kugelmitte. Die Position ist dabei abhängig von den Winkeln φ (zwischen r und Vertikale) und θ (zwischen r und Horizontalen). φ ist also verantwortlich für eine Links- oder Rechtsdrehung und der Winkel θ für eine Drehung der Kamera nach oben oder nach unten.
Die Transformationsgleichung für kartesische Kugelkoordinaten lautet:![]()
Die Koordinaten des Blickpunktes P lassen sich also in Abhängigkeit der Winkel folgendermaßen berechnen:
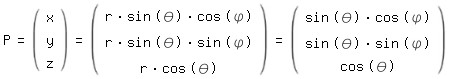
Bewegt man die Kamera in Richtung des Blickpunktes, kann man sich das als Bewegung entlang des Vektors ![]() vorstellen. Folgend der Code-Ausschnitt, welcher für die Bewegung der Kamera relevant ist:
vorstellen. Folgend der Code-Ausschnitt, welcher für die Bewegung der Kamera relevant ist:
/**
* Simulate flying camera
* */
void TerrainViewer::FlyingCamera()
{
double target_x, target_y, target_z;
//prevent camera from turning upside down
Viewer.cam_x_angle = Viewer.cam_x_angle > 179.5 ? 179.5 : Viewer.cam_x_angle;
Viewer.cam_x_angle = Viewer.cam_x_angle < 0.5 ? 0.5 : Viewer.cam_x_angle;
glViewport (0, 0, (GLsizei)width, (GLsizei)height);
glMatrixMode (GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0, (GLfloat) width / (GLfloat) height, 1.0, (GLfloat)(input.rows * input.grid_space * 4));
/* Move the point the camera looks at on a sphere.
* The viewing direction can be controled by the two angles cam_x_angle and cam_y_angle.
* */
target_x = Viewer.cam_x - sin(Viewer.cam_x_angle * PI / 180) * sin(Viewer.cam_y_angle * PI / 180);
target_y = Viewer.cam_y + cos(Viewer.cam_x_angle * PI / 180);
target_z = Viewer.cam_z - sin(Viewer.cam_x_angle * PI / 180) * cos(Viewer.cam_y_angle * PI / 180);
gluLookAt(Viewer.cam_x, Viewer.cam_y, Viewer.cam_z, target_x, target_y, target_z, 0.0, 1.0, 0.0);
glMatrixMode(GL_MODELVIEW);
}
Bedienung
Die Kamera lässt sich komplett mit der Maus steuern.
- Linke Taste: Wird die linke Maustaste gedrückt, kann die Richtung, in welche die Kamera blickt geändert werden. Eine Links- oder Rechtsbewegung ändert dabei den Winkel φ und eine Bewegung der Maus noch Oben oder Unten den Winkel θ.
- Rechte Taste: Mit der rechten Maustaste und einer Verschiebung der Maus, kann die Kameraposition in der Viewplane Ebene geändert werden.
- Linke + Rechte Taste: Klickt man die linke und rechte Maustaste gleichzeitig, kann die Kamera in der Horizontalen Ebene verschoben werden.
TerrainViewer
Download
Gallerie
Genfer See, Montblanc, Walliser Alpen

Level Of Detail

Fujisan Vulkan (Japan)
