Welcome to our project website!
Goals
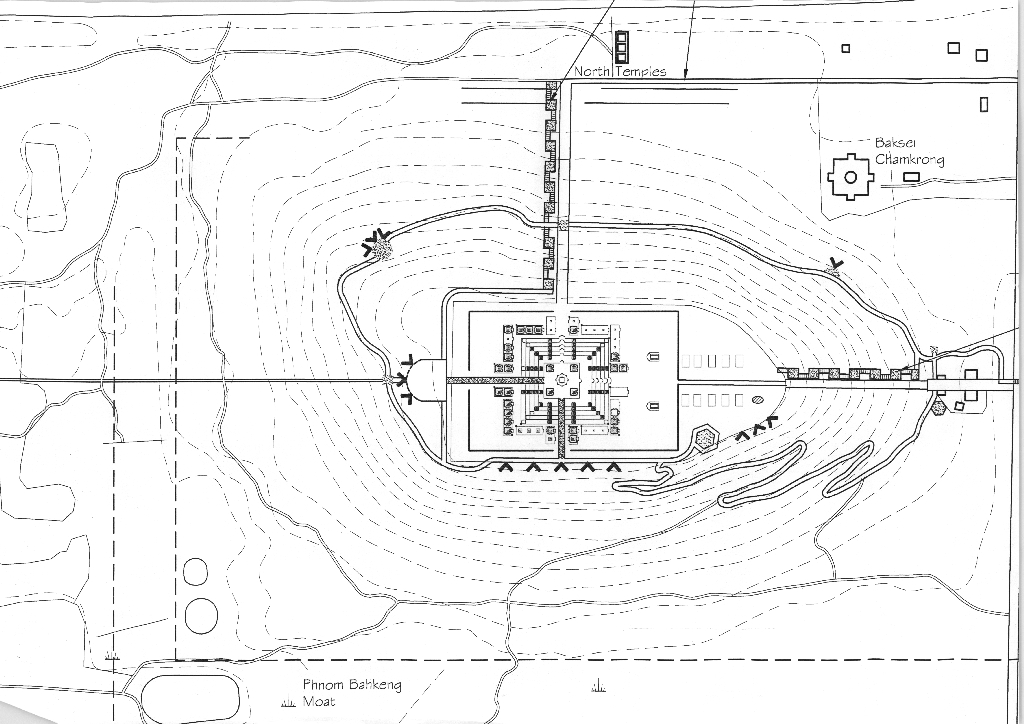
The starting point of our software project "Terrain Digitalization" was a (digital) topographic map of the Angkor temple area in Cambodia with several heightlines on it. Our task was to create a heightfield based on this map and the available height information. Furthermore the data type of the heightfield should be supported by Jens Rannacher's "TerrainViewer" to get a 3D-visualization of the temple area.
Theoretical foundations
HeightfieldIn computer graphics a heightfield (heightmap) is a two-dimensional data array representing the surface of a particular geographic place: each array element stores the height of the place described by its two array indices. Commonly heightfields are implemented as grayscale raster images with black representing minimum height and white representing maximum height. Heightfields are widely used in terrain visualization software, where they are converted into 3D meshes. We decided to offer two output formats of the heightfield in our program: a TIFF 16 bit grayscale image and an ArcGIS ASCII file. TIFF is a widespread well-supported picture format and with "LibTIFF" there is a free easy-to-use C library available allowing us to deal with TIFF files. The ArcGis ASCII format is supported by Jens Rannacher's "TerrainViewer".
Triangulation of a 2D-scatterplot
In order to get a formal specification of a 2D-triangulation we identify the drawing plane with the vector space R^2 over R and give the following topological definitions:
- Let M be a subset of
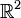. M is said to be convex if for every pair of points within M, every point on the straight line segment that joins them is also within M.
- Let M be a subset of 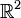. The convex hull conv(M) is is the minimal convex subset in 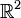containing M.
- A 2D-scatterplot P is finite subset of .
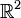A triangulation T(P) of a 2D-scatterplot P is a subdivision of the convex hull conv(P) into non-overlapping triangles such that their union is conv(P) and the vertices of the triangles coincides with the points of P.
Delaunay triangulation
In (computational) geometry a Delaunay triangulation DT(P) for a 2D-scatterplot P in the plane is a triangulation T(P) such that no point in P is inside the circumcircle of any triangle in DT(P). The Delaunay triangulation DT(P) maximizes the minimum angle of all possible triangulations for P. In terrain visualization, the Delaunay triangulation is often used to model the surface of a terrain described by a set of heightpoints, because it avoids narrow triangles due to the circumcircle condition.
Point localisation / linear height interpolation
This is explained in our report in the "Download" section.
Workflow
To extract the height information of the topographic map in an appropriate format we needed a raster graphics editor. We used "GIMP", because we wanted to use open source software available for various operating systems. In this way we produced a TIFF imagefile storing the height of each marked pixel as a gray scale value (see the "documentation"-section for further information). Pixels with unknown height remain unmarked and get the RGB value 0xffffff (white).Our C program reads this TIFF imagefile in order to interpolate a gray scale value for each remaining pixel based on the available height information. To do so, we first have to generate a 2D triangular mesh of the marked pixels. For this purpose we used Jonathan Shewchuk's free available program "Triangle", which we call within our program to get a Delaunay triangulation for our marked heightpoints.
After the successful call of the external "Triangle" our program sequentially determines for each pixel of the input imagefile, in which triangle of the Delaunay triangulation it is located. With the height values of the vertices of the located triangle it then interpolates the pixel height by a linear plane equation. In this way we obtain a complete heightfield storing a 16 bit gray scale pattern for the whole topographic map that can be used to render a 3D visualization of the Angkor temple area.
Introduction to external programs
Here is a short presentation of the external software we used in our project or which is needed to run our program:
- GIMP:
The GNU Image Manipulation Program (GIMP) is a raster graphics editor to process digital graphics and photographs. It is often used as a free software replacement for Adobe Photoshop. GIMP is an official part of the GNU project and available under the terms of the GNU General Public License.
You can get GIMP at the official website.
Notes for Mac users: We recommend using the packages provided by the "Wilber loves Apple" community on darwingimp.sourceforge.net. This is the easiest way to get GIMP for your Mac (only for Mac OS X 10.4 and 10.5). Running GIMP on Mac OS X requires Apple's X11 environment! Therefore be sure to read the install help in their download section. - LibTIFF: LibTIFF is a free available software distribution providing support for the Tag Image File Format (TIFF). The LibTIFF package comes with a C library, libtiff, for reading and writing TIFF, a small collection of tools for doing simple manipulations of TIFF images, and documentation on the library and tools. The official website is www.remotesensing.org/libtiff. If you want to build our program with the proviced source code, you have to link the libtiff library to our source files, because we use some of the C functions provided by libtiff. See the "documentation" section for further information on how to do this!
- Triangle: "Triangle" is a free available C program generating two-dimensional exact Delaunay triangulations, constrained Delaunay triangulations, conforming Delaunay triangulations, Voronoi diagrams, and high-quality triangular meshes. The official website is www.cs.cmu.edu/~quake/triangle.html. Our program expects "Triangle" to be in the same folder. Use our precompiled executables from the "Download" section. If you want to compile "Triangle" from source yourself, look at the official website for the source files and detailed help!