|
|
|
|
|
Stereographic projection
|
| |
|
Motivation
In a general context, the term "projection" simply refers to a mapping
π which has the property
π ° π = π, i.e. which does the same
when it is applied twice as when it is applied only once. Normally,
however, it also means that the map "reduces dimension" in some sense
that suits the specific context.
Since we only deal with Rn in the very moderate case where
n ≤ 4, the only projections of interest are maps from
R4 to R3 and from R3 to R2.
Of course we consider R3 embedded in R4, e.g by
R3 x {0} ⊆ R4 (and
similarly for one dimension below). Therefore, the first and most
obvious candidate for a projection is the map that simply discards the
last coordinate (this works well in both cases). Note that it
obviously has the above mentioned property
π ° π = π.
This is indeed a valuable map, but it has the great disadvantage of
smashing the sphere to a disk. That means, it does not map it
injectively into the plane (it may sound strange to look for a map
that reduces dimensions and is still injective on the sphere, but read
on). Additionally, we would like to work with a slightly more complex
one which adds a little more spice to our pictures.
Looking for an interpretation of our first map we see that, when
applied to a configuration of objects in R3, it sort of
"flattens them down" to the plane. Imagine the sun shining vertically
down on the plane. Then the image of an object is its shadow on the
plane.
Why not slightly modify this idea by letting the source of light being
a light bulb (idealized as a point) instead of the sun? Then the rays
of light emerge from a single point rather than being parallels
emitted by the point at infinity. This is exactly the approach we will
take and the resulting map is called "stereographic projection".
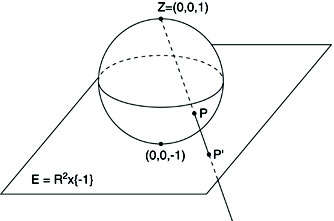
Definition
We will now formalize our ideas and first consider the 3-dimensional
case in order to get a grip of the ideas. The generalization to
4 dimensions will be immediate.
As above, we consider the plane R2 embedded in
R3, but this time we move the plane one unit "down":
E=R2 x {-1} ⊆ R3. This
has technical reasons and is not relevant at all, as we will see
later. As the "source of light" we choose the point Z located on the
z axis two units above the plane. Now for any point
P ≠ Z we consider the line l joining Z and P. If it
happens not to be parallel to E, there is a point of intersection of l
and E which we will call P'. This is the image of P under
stereographic projection with center Z (for an illustration see
the picture below).
Obviously this map seems to be considerably more interesting than the
simplistic projection above. And a quick thought convices us that the
unit sphere is in this case indeed mapped injectively into the plane
(of course, we must exclude the "north pole" whose image is not
defined). In fact, the map provides even a bijection between
the sphere (minus the north pole) and the plane. This is an important
fact to remember.
On the other hand, can we describe the map in a sufficiently easily
handable way or is it too complicated to be dealt with? The answer is
surprising. The only ingredient we need do derive a formula is
elementary geometry. Let the coordinates of P be p1, p2, p3, and
denote the coordinates of P' by q1, q2, q3 (trying to avoid confusion
I will desist from calling them p'1, p'2 and p'3...). Since P' lies in
E, q3 is of course equal to -1.
If we draw virtual "horizontal" lines from P and P' to the points
R=(0,0,p3) and S=(0,0,q3) respectively, then the two triangles ZPR and
ZP'Q are similar (since PR and P'S are parallel). Thus,
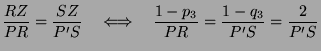
Applying a similar argument to the lines PR and the coordinates p1,
p2, as well as to P'S and q1, q2, we obtain the final formula (π
denotes the stereographic projection)
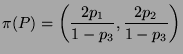
From this it can also rigorously be derived that the map restricted to
the sphere minus the north pole (whose third coordinate equals 1, thus
for which no image is defined) is indeed bijective. By the way, if we
had chosen the plane R2 x {0} instead of
R2 x {-1}, the only difference would have been
that the 2 in the numerator would have to be changed to a 1 (the
argument is exactly analogous to the one above).
Now the generalization to 4 dimensions is indeed
obvious. The formula is given by
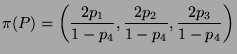
and swift caclulations yield analogous properties. In
particular is the 3-sphere (minus the point (0,0,0,1) bijectively
mapped to R3 x {-1}).
|
| |
|
|
|

