So far we have been introduced to the Hopf map as well as to stereogaphic projection. But what do they have to do with each other and with our aim to visualize the 3-sphere? This section holds the answer.

As I said, the final goal is to visualize the 3-sphere S³. The introduction has already mentioned the fundamental problem of finding good subsets of S³ fitting this purpose, for simply projecting the whole hypersphere would leave us with R³, which doesn't get us far.

This is where the Hopf map comes in. The hypersphere is the preimage of the ordinary sphere under the Hopf map. If we take the preimage only of a subset of the sphere, we accordingly obtain a subset of the hypersphere, and these subsets are sufficiently interesting to lead to interesting pictures in the end.

From the section about the Hopf map we learned that the preimage h^-1(P) of a point P on S² is a circle on S³. Now we extend the point to a whole circle C on S². Then its preimage h^-1(C) will be a family of circles on S³, and this family happens to comprise a torus, which is contained entirely in S³. We won't consider yet more complicated subsets of S² since circles are the only ones that are still easy to describe (they are determined by their plane of intersection with S², which is given by as few data as its normal vector and its distance from the origin).

A possibility which lies somewhere in between is to consider only a finite set of equally distributed points on such a circle C instead of the entire circle. The preimages of these points consist of a number of pairwise linked circles.


So far the Hopf map has supplied us with a certain subset of S³. But S³ is still a set in R⁴, which is one dimension too high for us to imagine. This is why we now need to project this specific subset into R³ by means of stereographic projection. As already mentioned in the corresponding section, stereographic projection can also be interpreted as inversion with respect to a sphere. The latter map has the property to map circles to circles (where the definition of "circle" is extended to include lines). Thus when we project a circle that was obtained as the preimage of some point, the result is another circle, but this time in R³. Its exact position can be derived by simple elementary geometric observations, but we won't go into detail here. Further information is provided in the algorithms section.

The second kind of "hypersubset" (i.e. subset of the hypersphere) we obtained above was a torus on S³. This, when projected into R³, results in a geometric object known as "Dupin cyclide". It is a well known object for which explicit parametrizations are known.
HyperView uses the results of Rimvydas Krasauskas (see the links section) that provide a parametrization with two projective parameters. In HyperView each of those is split into a chart of two affine parameters, however. In this way we obtain four surface patches each of which is drawn using OpenGL evaluators (i.e. Bézier surfaces). A picture illustrating this as well as details about the exact process can be found in the algorithms section.
A footnote in between: It might be true that a single surface patch be sufficient using the OpenGL NURBS interface. This is beyond my present understanding, however. If you have any ideas how to realize this, please mail me.

Finally, if we restrict our attention to some points on a circle C contained in S² instead of considering C as a whole, their preimages is a number of pairwise linked circles on S³, as already explained earlier. Projecting these into R³ again yields again a number of pairwise linked circles every one of which lies on the surface of the Dupin cyclide that would result as the projection of h^-1(C). Drawing these circles provides a "skeleton" of the cyclide in some sense. Examples for this can be found in the screenshots section, e.g. on the first picture.


In order to make things entirely clear, here is a schematic summary of what is going on in HyperView.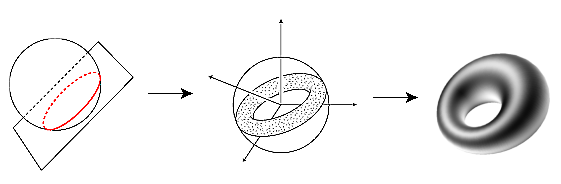



First, a circle on S² is taken (leftmost picture, in red; for illustration, its plane of intersection is drawn as well). Its preimage under the hopfmap yields a torus on S³ (picture in the middle; since drawing in four dimensions exceeds my capabilities, I have incidated the fourth dimension by a fourth coordinate axis which is almost orthogonal to the other three :-) This torus is in turn projected back to R³ yielding a Dupin cyclide.