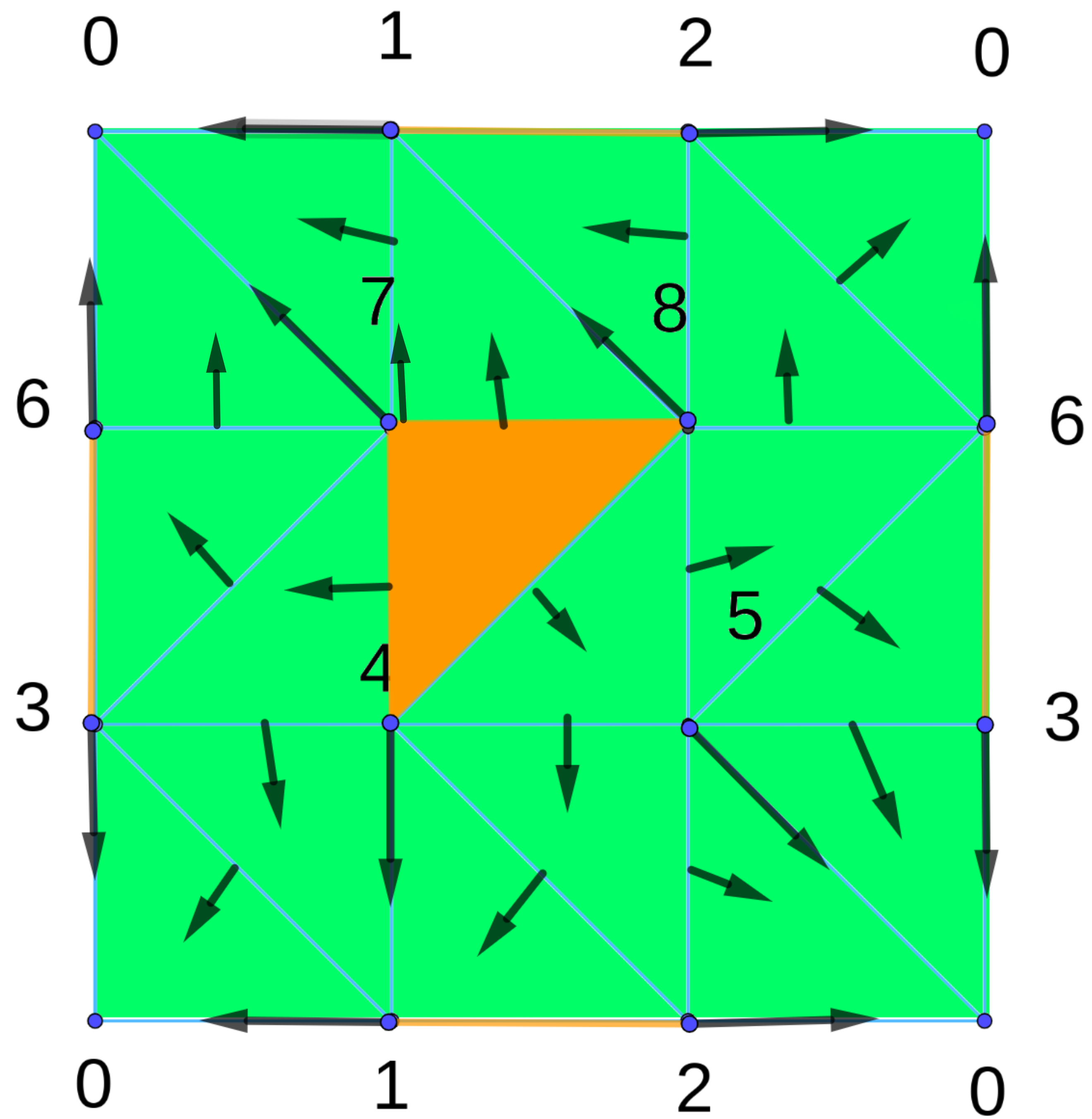
Requirments of algorithm
The algorithm processes the lower star of vertices of a simplicial complex. A lower star of a vertex x in a simplicial complex $\mathcal{K}$ with scalar value g defined on vertices of $\mathcal{K}$ is the set of all simplices containing x as a vertex and if $\beta$ is a simplex containing x as a vertex then the scalar value of x is greater than or equal to the scalar value of any other vertex of $\beta$. Here is the mathematical definition of lower star set:
$L(x)=\{\beta \in \mathcal{K} \mid x \in \beta \: and \: \max\limits_{v \in \beta} \: g(v) \leq g(x)\}$
$L(0)=()$
$ L(1)=(\overline{10})$
$ L(2)=(\overline{20},\overline{21})$
$ L(3)=(\overline{30},\overline{31},\bigtriangleup(310))$
$ L(4)=(\overline{41},\overline{42},\bigtriangleup(421), \overline{43},\bigtriangleup(431))$
$L(5)=(\overline{50},\overline{52},\bigtriangleup(520),\overline{53},\bigtriangleup(530),\overline{54},\bigtriangleup(542))$
$L(6)=(\overline{60},\overline{62},\bigtriangleup(620),\overline{63},\overline{65},\bigtriangleup(653))$
$L(7)=(\overline{70},\overline{71},\bigtriangleup(710),\overline{73},\overline{74},\bigtriangleup(743),\overline{76},\bigtriangleup(760),\bigtriangleup(763))$
$L(8)=(\overline{81},\overline{82},\bigtriangleup(821),\overline{84},\overline{85},\bigtriangleup(854),\overline{86},\bigtriangleup(862),$
$\bigtriangleup(865),\overline{87},\bigtriangleup(871))$
Notice, that the vertices are labeled by their scalar value $g$. Other cells are labeled by their vertices in decreasing order, for example a cell $\alpha =\{1,2,3\}$ will be labeled (321) and can not be labeled in other way.
The algorithm

Example
We process the lower star of each vertex (the order does not matter). We begin with vertex 0. $L(0) =\{\}$ so 0 will be added to critical points. Now, we process vertex 1. $ L(1)=(\overline{10})$, we pair 1 with $\overline{10}$ and so L(1) is done. Then we process vertex 2. $ L(2)=(\overline{20},\overline{21})$ vertex 2 is paired with edge $\overline{20}$ and edge $\overline{21}$ is added to PQzero. PQone is empty. Since PQzero contains only $\overline{21}$, so it will be added to critical cells. So L(2) is done. $ L(3)=(\overline{30},\overline{31},\bigtriangleup(310))$. The vertex 3 will be paired with edge $\overline{30}$. The edge $\overline{31}$ will be add to PQzero since its face in lower star has been paired (we consider only faces according lower star, here face 3 face 0 does not apply) and $\bigtriangleup(310)$ will be inserted in PQone since it has only one unpaired face, namely $\overline{31}$. Now, we iterate in PQone and remove $\bigtriangleup(310)$ and pair it with its pair $\overline{31}$. Repeating the algorithm on all other vertices, we will get the the critical cell list $C = \{0, \overline{21}$,$\overline{63}$,$\bigtriangleup(874)\} $that match our expectations and the discrete vector field $V = \{1:\overline{10},2:\overline{20}, 3: \overline{30},4:\overline{41},5:\overline{40},6:\overline{60},7:\overline{70},8:\overline{81} ,\overline{31}:\bigtriangleup(310),\overline{43}:\bigtriangleup(431),\overline{42}:\bigtriangleup(421),\overline{54}:\bigtriangleup(542),\overline{52}:\bigtriangleup(520),\overline{53}:\bigtriangleup(530),\overline{73}:\bigtriangleup(763),\overline{74}:\bigtriangleup(743),\overline{84}:\bigtriangleup(854),\overline{85}:\bigtriangleup(865),\overline{65}:\bigtriangleup(653),\overline{76}:\bigtriangleup(760),\overline{71}:\bigtriangleup(710),\overline{87}:\bigtriangleup(871),\overline{82}:\bigtriangleup(821),\overline{86}:\bigtriangleup(862),\overline{62}:\bigtriangleup(620)\}$. The illustration of critical cells and discrete vector field are shown in next figure.