Chosen Models
Most objects can be displayed in 3D and those formulas exist, but there had to be adjustments to make it fit the framework. PlyFile has a very specific format, and 3D-HOP can read either PlyFile objects, or compressed files in the Nexus Format.
Since the PlyFile format is quite simple to grasp, (as seen here), it was chosen for this project.
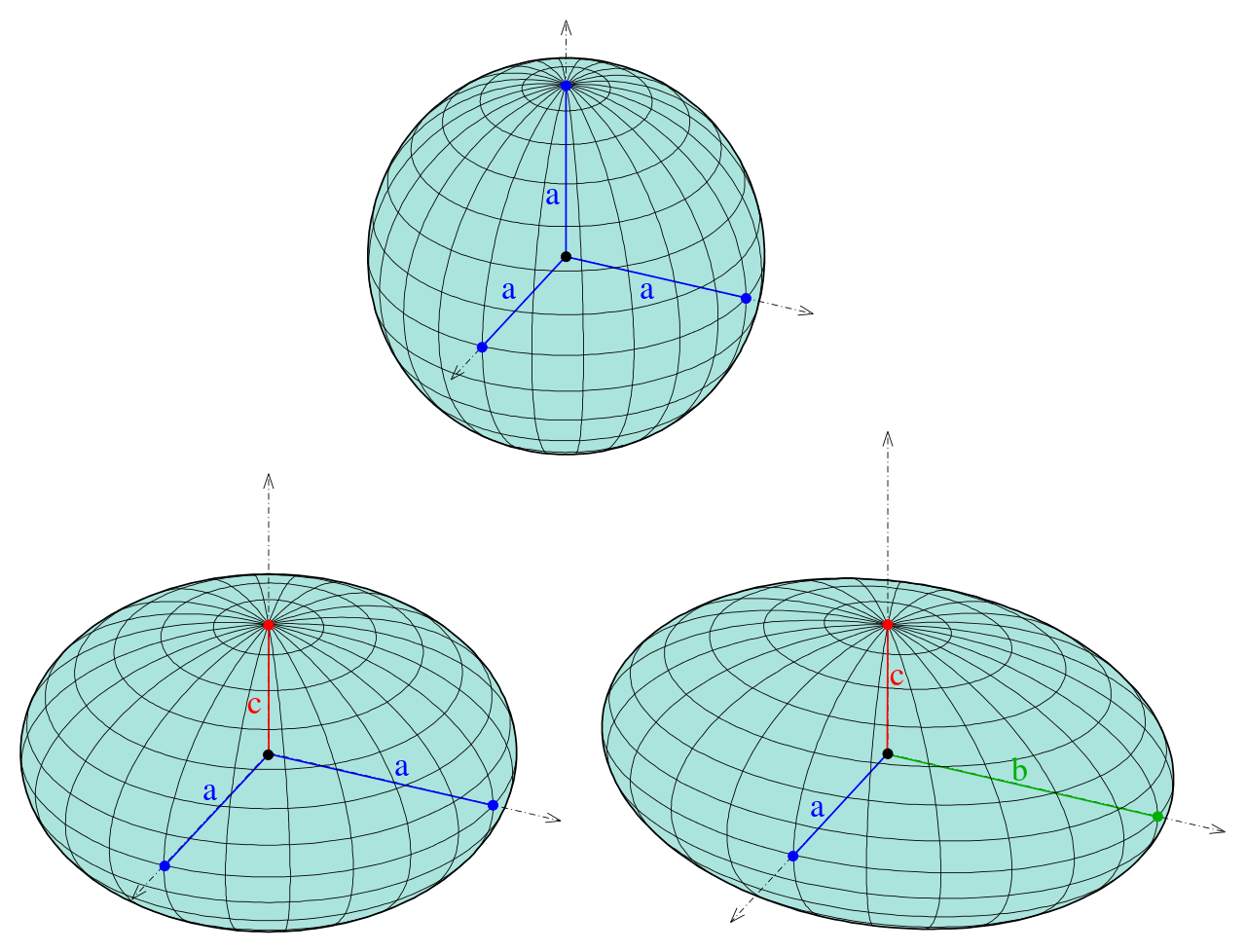
Ellipsoid
This is one of the most basic 3D-Objects one could create.
| An Ellipsoid can be displayed in cartesian coordinates. |
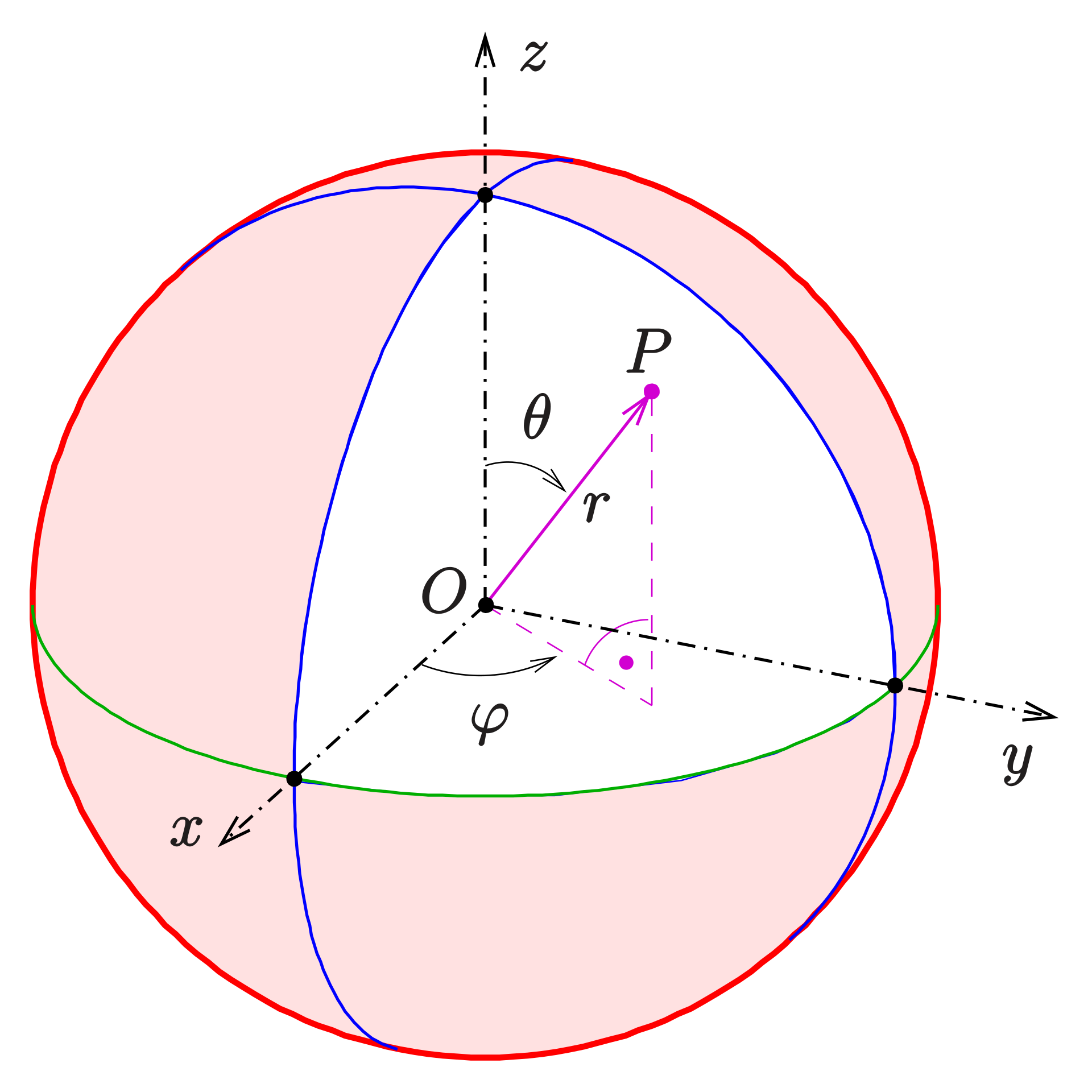
To properly parameterize it, you can use spherical coordinates, with the elliopsoid axes coinciding with the coordinate axes. In that case the coordinates would be calculated as followed:
|
y = b sin θ cos φ z = c cos θ |
|
The variables a, b and c stand for the length of the corresponding axis.
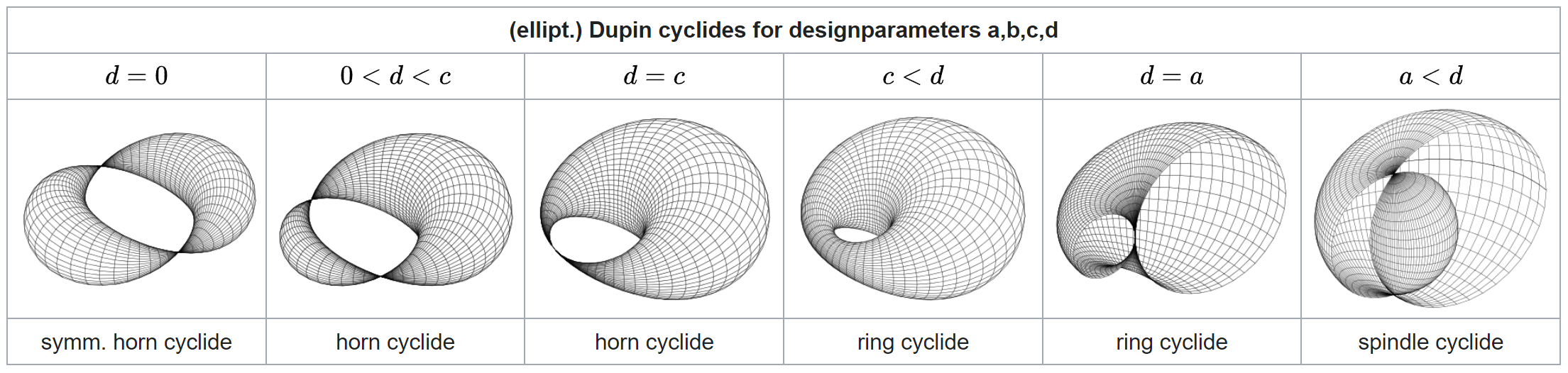
Dupin Cyclide
A Dupin cyclide is constructed by "inverting" a cylinder, cone or a standard torus in a sphere. Therefore they are natural objects in Lie sphere geometry. Here the curvature lines are either circles or lines.
| x = (d + c cos θ
) cos φ y = (d + c cos θ ) cos φ z = c sin θ |
There are many different looking Dupin cyclide. The models chosen were the Horn cyclide, which is the elliptic case and the Dupin cyclide in the parabolic case, here abbreviated to Parabolic cyclide.
Horn Cyclide
The variables a, b, c need to comply with the following restrictions:
a < b < c, c2 = a2 - b2
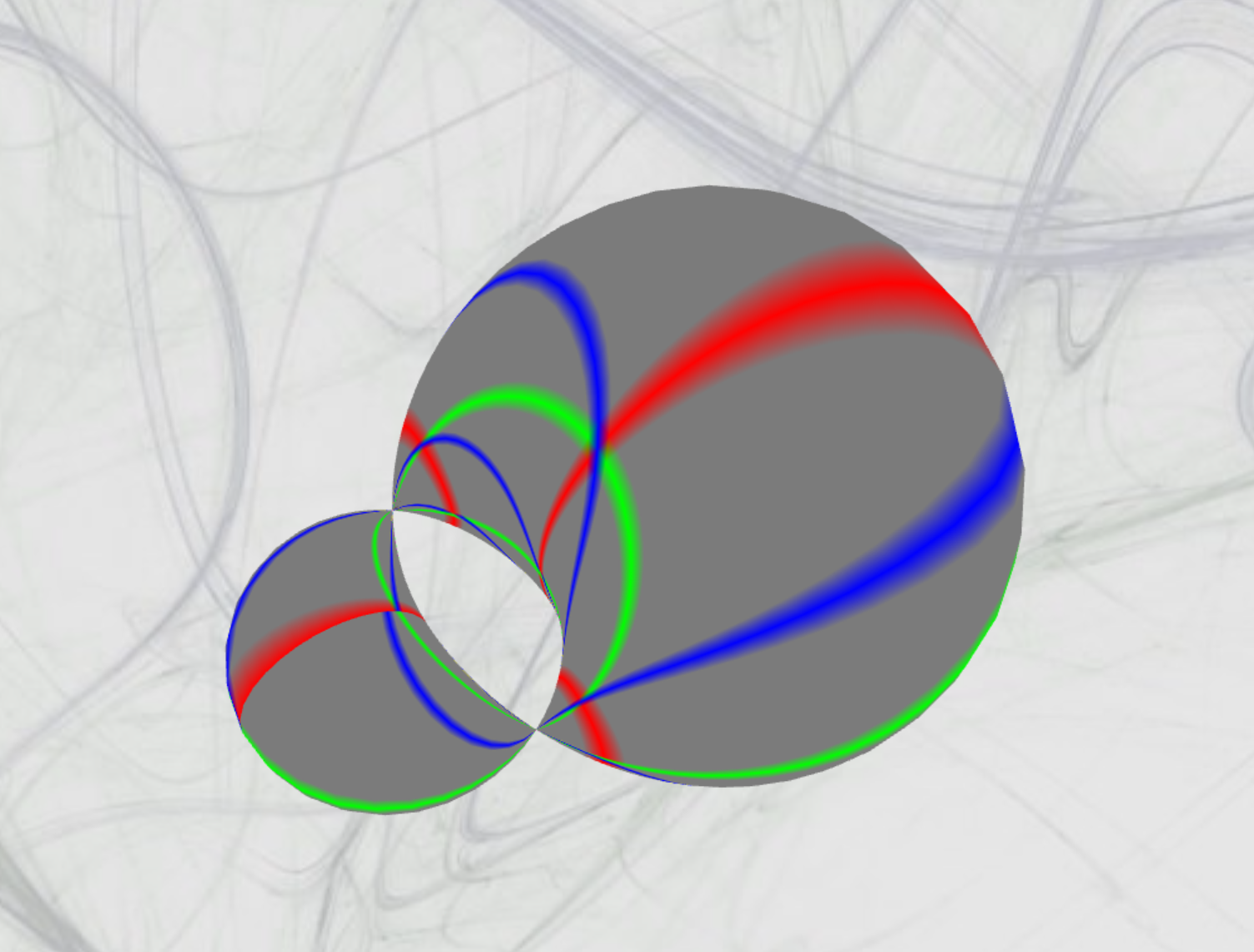
Parabolic Cyclide
With following restrictions: -∞ < u, v > ∞
With a parabolic Cyclide the centre of the sphere of inversion lies on the torus.
 |
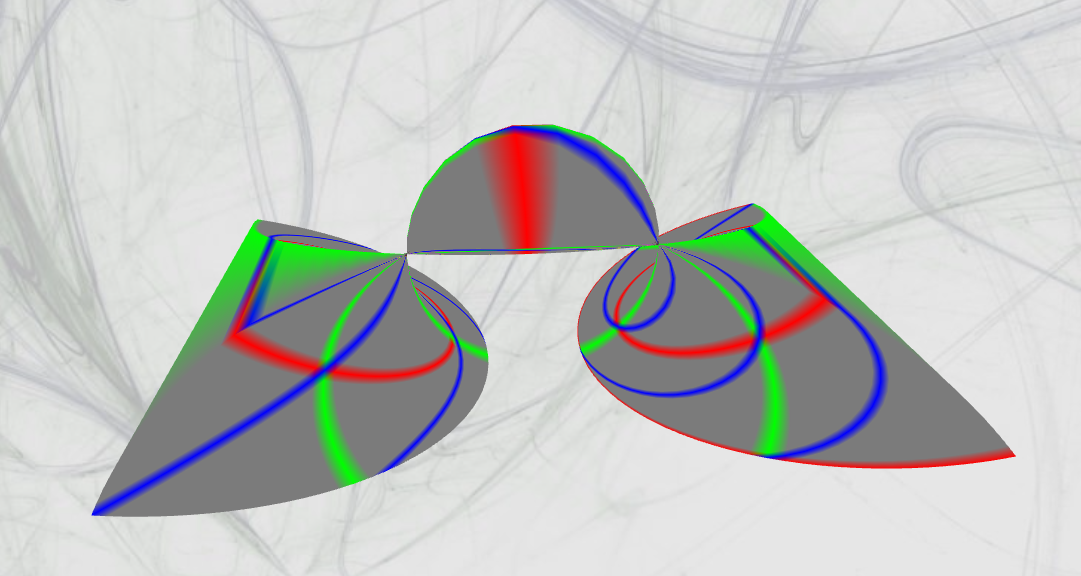 |
| Model from this Project for a Parabolic Cyclide, single colored, displayed in an average 3D-program | Model from this Project for a Parabolic Cyclide, as seen on the product, with curvature lines in the early stages of development |
Hyperboloid
|
|
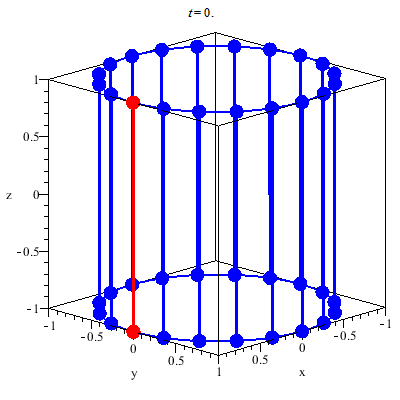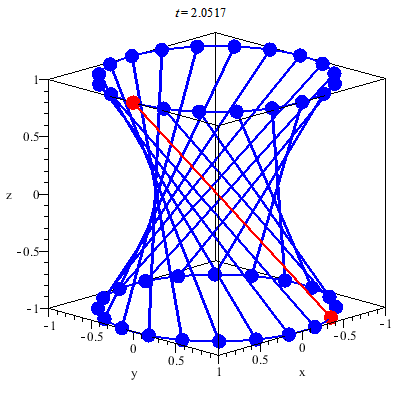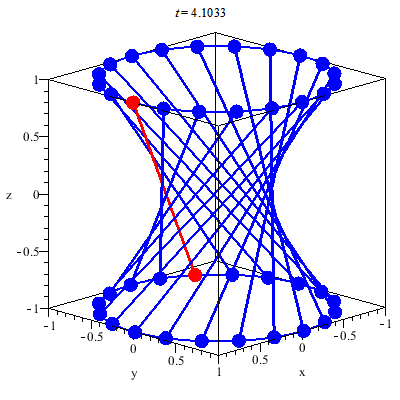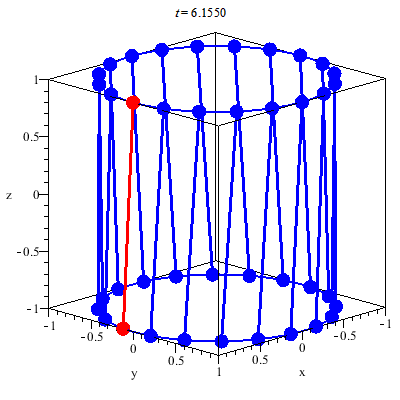 |
Depending on variable d the hyperboloid will look different:
| d > 0 | Hyperboloid with one sheet |
| d < 0 | Hyperboloid with two sheets |
| d = 0 | double cone |