Kiretu

Class description

Kiretu contains four classes for creating a point cloud:

This page describes the functionality of the classes. It concentrates on the theoretical background of the classes. For aspects of programming see Data Structures.

YMLParser

The YMLParser imports the Kinect specific calibration file which includes the Kinect’s extrinsics and the depth- and RGB-camera’s intrinsics. Afterwards, it parses all the parameters.

FrameGrabber

The FrameGrabber captures frames of the depth- RGB-camera. One problem of the depth-stream is image noise (concerning the depth-values). You can see this at the glview depth map:

I analyzed this issue capturing the following test scene showing objects with different materials and degrees of reflection:

test-scene.png

To get as many valid depth-values as possible, the FrameGrabber is able to grab a variable number of frames (images). A depth-value 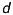$ d $ is called valid, if 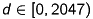$ d \in [0, 2047) $. After grabbing all frames, it computes the mean of each pixel’s valid depth values.

Here you can see relation between the number of frames and points (concerning the test scene):

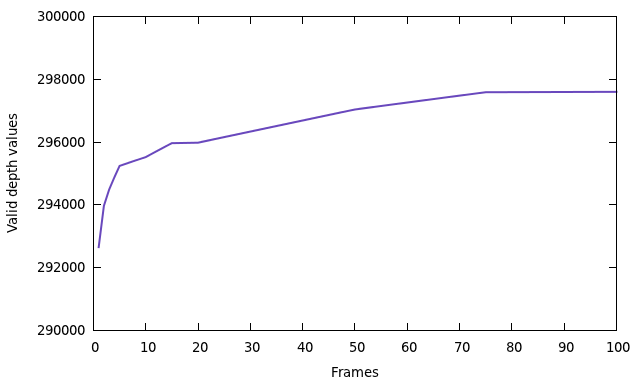
numberframes-validvalues.png

I choose 50 frames as a compromise between the number of points and the time of capturing.

A problem occurs, if the depth values of a pixel vary too much over the frames. E. g. the pixels at an object’s edge, which switch between the object’s depth and background’s depth behind the object. You can see this effect in the following two images. Both show a point cloud of the test scene. At the first picture, only one frame was captured. The second image shows the problematic points after taking the mean of 50 frames.

numberframes-points-1-frame.png
numberframes-points-50-frame.png

The affected points are characterized by highly varying depth values. As measure of this diversity is the standard deviation [1]. For this reason it is useful to take a look at the frequency of the standard deviation of the depth values around the equivalent mean:

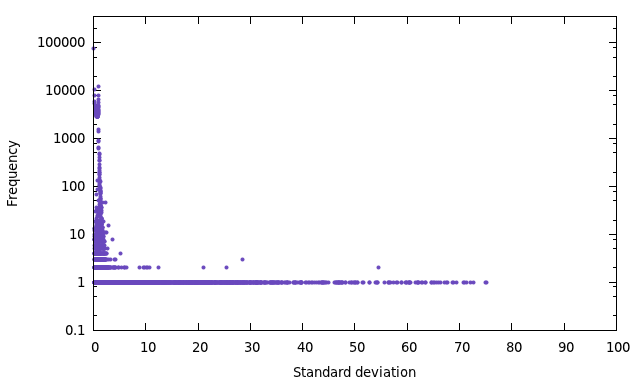
sd-frequency.png

Now, the idea is to use the standard deviation 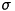$\sigma$ as a threshold to recognize and sort out problematic points. This implicates, that the value of 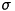$\sigma$ determines the final number of points. Here you can see the total number of points depending on the standard deviation:

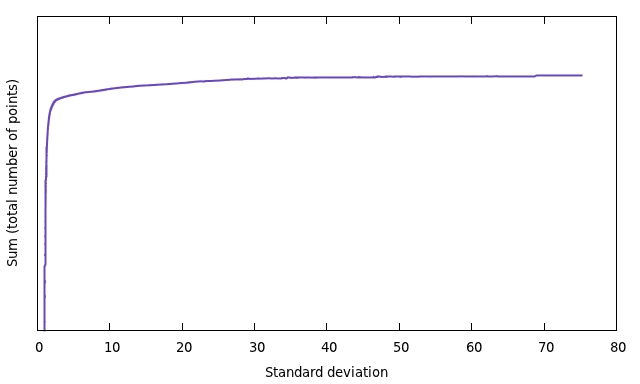
sd-sum.png

I choose 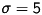$\sigma = 5$ as the default value.

Finally, the question is, how many valid values can be achieved by this optimization. Here are the results (maximum 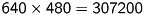$ 640 \times 480 = 307200 $):

1 frame 292650 points
50 frames without threshold 297038 points (+4388, 1.5 %)
50 frames with threshold 295461 points (+2811, 1.0 %)

KinectCloud

Based on the content of Reconstruction, this section explains how the reconstruction of the point cloud is done by KinectCloud.

Important: All references to equations refer to the numbers given in Reconstruction.

Step 1: Raw to meter

First, you have to convert the raw depth-values of Kinect ( $ Z_\mathsf{raw} \in [0, 2047] $) into meters. This is done by the following, experimental determined formula [2]:

\[ Z_\mathsf{meter} = \frac{1}{Z_\mathsf{raw} \cdot (-0.0030711016) + 3.3309495161} \]

Step 2: Depth to cloud

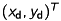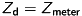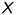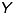Then, we project the depth-image into the threedimensional space. Let $ (x_\mathsf{d}, y_\mathsf{d})^T $ be a pixel at the captured depth-image and $ Z_\mathsf{d} = Z_\mathsf{meter} $ the depth value of the pixel, converted into meter. Using equation (5), the $X$- and $Y$-coordinate of the equivalent threedimensional point 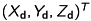$ (X_\mathsf{d}, Y_\mathsf{d}, Z_\mathsf{d})^T $ can be computed as follows:

\begin{align*} \begin{pmatrix} x_\mathsf{d} \\ y_\mathsf{d} \\ 1 \end{pmatrix} &= \begin{pmatrix} f_x & 0 & c_x & 0 \\ 0 & f_y & c_y & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} X_\mathsf{d} \\ Y_\mathsf{d} \\ Z_\mathsf{d} \\ 1 \end{pmatrix} \\ \Leftrightarrow\ \begin{pmatrix} x_\mathsf{d} \\ y_\mathsf{d} \\ 1 \end{pmatrix} &= \begin{pmatrix} f_xX_\mathsf{d} + c_xZ_\mathsf{d} \\ f_yY_\mathsf{d} + c_yZ_\mathsf{d} \\ Z_\mathsf{d} \end{pmatrix} \stackrel{\mathsf{(4)}}{=} \begin{pmatrix} f_xX_\mathsf{d}/Z_\mathsf{d} + c_x \\ f_yY_\mathsf{d}/Z_\mathsf{d} + c_y \\ 1 \end{pmatrix} \\[0.5cm] X_\mathsf{d} &= \frac{(x_\mathsf{d} - c_x) \cdot Z_\mathsf{d}}{f_x},\quad Y_\mathsf{d} = \frac{(y_\mathsf{d} - c_y) \cdot Z_\mathsf{d}}{f_y} \end{align*}

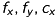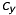Regard, that $f_x, f_y, c_x$ and $c_y$ are the parameters of the depth-camera!

Step 3: Apply extrinsics

The point cloud is given in coordinates of the depth-camera’s coordinate system. We now have to transform all points to the RGB-camera’s coordinate system. This is done by applying the extrinsic parameters to each point:

\[ \begin{pmatrix} X_\mathsf{rgb} \\ Y_\mathsf{rgb} \\ Z_\mathsf{rgb} \end{pmatrix} = \begin{pmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{pmatrix} \begin{pmatrix} X_\mathsf{d} \\ Y_\mathsf{d} \\ Z_\mathsf{d} \end{pmatrix} + \begin{pmatrix} t_1 \\ t_2 \\ t_3 \end{pmatrix} \]

Step 4: RGB mapping

Finally, we reproject the point cloud onto the RGB-image to get the equivalent color of each point. Therefor, we can use equation (5), again. Let 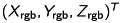$ (X_\mathsf{rgb}, Y_\mathsf{rgb}, Z_\mathsf{rgb})^T $ be the point in the space. We can compute the corresponding pixel 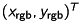$ (x_\mathsf{rgb}, y_\mathsf{rgb})^T $ at the RGB-image as follows:

\begin{align*} \begin{pmatrix} x_\mathsf{rgb} \\ y_\mathsf{rgb} \\ 1 \end{pmatrix} &= \begin{pmatrix} f_x & 0 & c_x & 0 \\ 0 & f_y & c_y & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} X_\mathsf{rgb} \\ Y_\mathsf{rgb} \\ Z_\mathsf{rgb} \\ 1 \end{pmatrix} \\ \Leftrightarrow\ \begin{pmatrix} x_\mathsf{rgb} \\ y_\mathsf{rgb} \\ 1 \end{pmatrix} &= \begin{pmatrix} f_xX_\mathsf{rgb} + c_xZ_\mathsf{rgb} \\ f_yY_\mathsf{rgb} + c_yZ_\mathsf{rgb} \\ Z_\mathsf{rgb} \end{pmatrix} \stackrel{\mathsf{(4)}}{=} \begin{pmatrix} f_xX_\mathsf{rgb}/Z_\mathsf{rgb} + c_x \\ f_yY_\mathsf{rgb}/Z_\mathsf{rgb} + c_y \\ 1 \end{pmatrix} \\[0.5cm] x_\mathsf{rgb} &= \frac{f_xX_\mathsf{rgb}}{Z_\mathsf{rgb}} + c_x,\quad y_\mathsf{rgb} = \frac{f_yY_\mathsf{rgb}}{Z_\mathsf{rgb}} + c_y \end{align*}

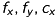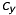Regard, that $f_x, f_y, c_x$ and $c_y$ are the parameters of the RGB-camera!

Summary

For better understanding, here is a summary of the four reconstruction steps:

  1. Raw to meter (M): Convert the depth values of the Kinect’s depth image into meter.
  2. Depth to cloud (D): Project the pixels of Kinect’s depth image into the space using the corresponding depth value.
  3. Apply extrinsics (E): Transform all points to the RGB-camera’s coordinate system.
  4. RGB mapping (R): Reproject the point cloud to the RGB-image.

CloudWriter

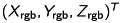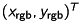The CloudWriter generates and saves a ply point cloud. Every point $ (X_\mathsf{rgb}, Y_\mathsf{rgb}, Z_\mathsf{rgb})^T $ of the cloud gets assigned to its corresponding color value of the RGB-image with the coordinate $ (x_\mathsf{rgb}, y_\mathsf{rgb})^T $.

Because of the different positions/orientations of the depth- and RGB-camera, it is possible, that points without a corresponding color exist. It is possible to discard them or print them in a user-defined color.

The reconstruction-steps are recognizable in the filename, e. g. 

cloud-2012-01-16-17-27-51-M-D-E-r.ply

where M, D, E and r relate to the reconstruction-steps as described at the summary above and upper case indicates an executed reconstruction-step, while lower case means the opposite.

Wikipedia (engl.): Standard deviation. http://en.wikipedia.org/wiki/Standard_deviation [2012-01-22]
Burrus, Nicolas: Kinect Calibration. http://nicolas.burrus.name/index.php/Research/KinectCalibration [2012-01-22]
Author:
Daniel Wunderlich (d.wunderlich@stud.uni-heidelberg.de)
Date:
2012-01-26
 All Data Structures Files Functions Variables Enumerations Enumerator
[Page Up]