Einführung FaceCenterPoints Zyklenberechnung VESTA-Zyklen Triangulierung Abstandsgesetz Ergebnisse Ausblick Anwendung Quellennachweise
Wenn man aus einem dreidimensionalen skalaren Feld eine Oberfläche extrahieren will, dann muss man sich als erstes darüber klarwerden, wo diese Oberfläche verlaufen soll. Eine sinnvolle Grenzfläche wird naheliegenderweise dadurch definiert, dass man alle Punkte, denen derselbe Zahlenwert zugeordnet wird, zu eben dieser Fläche zählt - was natürlich nur dann eine sinnvolle Fläche ergibt, wenn das skalare Feld ein Kontinuum darstellt und stetig ist. Eine derartige Fläche wird als Isofläche bezeichnet und lässt sich formal definieren als die Fläche
![\[ \mathlarger{\mathlarger{ S = \{ v \in \mathbbm{R}^3 \, \vert \; \varphi (v)=c \text{ mit } \varphi : \mathbbm{R}^3 \to \mathbbm{R}, \varphi \text{ stetig, } c \in \mathbbm{R} \} }} \]](form_18.png)
Im Zweidimensionalen hat sie eine Entsprechung in der Isolinie, die in der Form der Isobaren auf Wetterkarten ihre größte Bekanntheit erlangt haben dürfte. Dort verbindet sie alle Punkte gleichen Luftdrucks. Der Zahlenwert c, der die Isofläche definiert, wird im folgenden als Isowert bezeichnet.
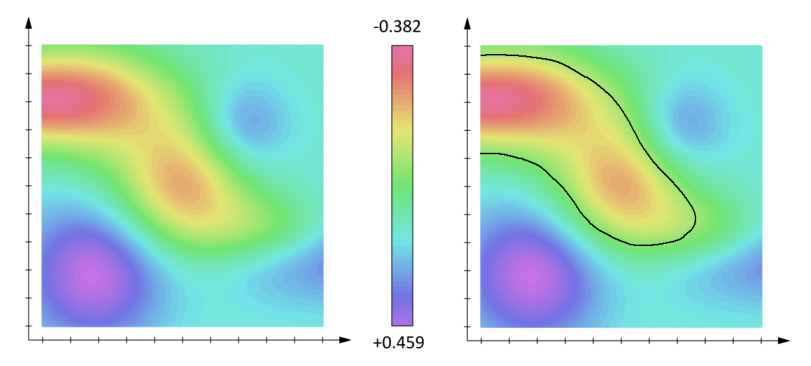
Das skalare Feld liegt uns in der elektronischen Datenverarbeitung naturgegebenermaßen nur in diskretisierter Form vor. Im ILATO-Projekt ergeben sich beispielsweise die diskreten Werte aus der CT-Messung, die jeder Voxel-Zelle einen mittleren Dichtewert zuweist. Diese Werte werden dann als die Dichtewerte der punktförmigen Voxelzentren interpretiert. Somit erhalten wir ein dreidimensionales, quaderförmiges Gitter, in dem den einzelnen Gitterpunkten jeweils ein bestimmter Wert zugeordnet wurde.
Die Punkte, die zu einem vorher festgelegten Isowert gehören, stellen nun im allgemeinen keine Gitterpunkte dar. Da aber angenommen wird, dass das skalare Feld stetig ist, gilt der Zwischenwertsatz, und das bedeutet, dass es zwischen zwei benachbarten Gitterpunkten, deren Dichtewerte so beschaffen sind, dass der eine über dem Isowert, der andere aber unter dem Isowert liegt, stets mindestens einen Punkt gibt, dessen Wert mit dem Isowert identisch ist. Die genaue Lage eines derartigen Punktes lässt dich dann mithilfe linearer Interpolation abschätzen.
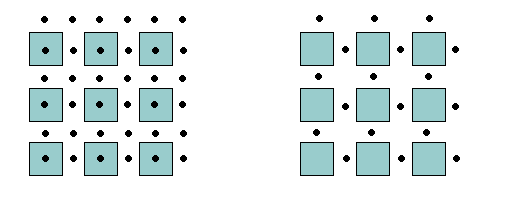
Wenn man nun sukzessive alle benachbarten Voxelzentren daraufhin überprüft, ob sich zwischen ihnen ein derartiger Punkt befindet, erhält man eine Menge von Punkten, die alle auf der Isofläche liegen. Diese Punkte werden im folgenden Face Center Points genannt (ein Begriff, der auf der nächsten Seite erklärt wird). Verbindet man jeweils zwei benachbarte Face Center Points, so kann man annehmen, dass auch diese Verbindungslinie in der Nähe des Isowertes verläuft. Ebenso ist eine Fläche, die von derartigen Verbindungslinien begrenzt wird, eine gute Annäherung an die Isofläche. Das Ganze lässt sich anhand folgender Abbildung illustrieren:
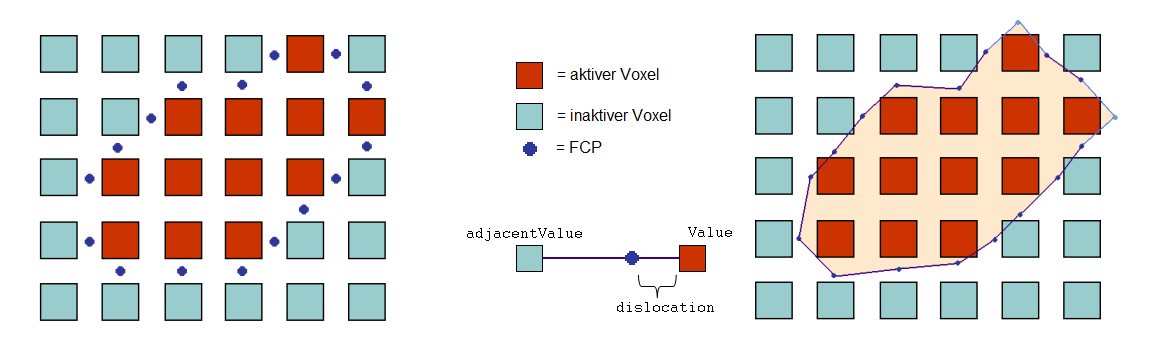
Die Abbildung beschränkt sich auf den zweidimensionalen Fall. Die Voxel werden durch blaue und rote Kästchen repräsentiert, die in einem Rechteck angeordnet sind. Alle Voxel, deren Wert unter dem Isowert liegen, werden im folgenden als inaktiv bezeichnet und sind blau eingefärbt, die restlichen Voxel werden aktiv genannt und sind rot eingefärbt. Die Face Center Points liegen nun jeweils zwischen einem aktiven und einem inaktiven Voxel - allerdings nicht in diagonaler Richtung, sondern nur in x- oder y-Richtung. Im linken Teil der Abbildung wurde angenommen, dass die Position der Face Center Points jeweils genau in der Mitte zwischen einem aktiven und einem inaktiven Voxel liegt - was nur dann der Fall ist, wenn der Isowert für die zu extrahierende Fläche genau in der Mitte zwischen den Werten der aktiven und inaktiven Voxeln liegt (also zum Beispiel dann, wenn allen aktiven Voxeln der Wert 100, allen inaktiven der Wert 0 und der zu extrahierenden Fläche der Wert 50 zugeordnet wurde). Da dies nur sehr selten der Fall sein dürfte, müssen die Face Center Points in der Regel längs der Verbindunglinie zwischen den benachbarten Voxeln verschoben werden. Der Abstand von dem aktiven Voxel beträgt dabei stets:
wobei value der Wert des aktiven, adjacentValue der Wert des inaktiven Voxels und isoValue der Isowert der zu extrahierenden Oberfläche ist. An dieser Stelle sei schon darauf hingewiesen, dass dislocation niemals 0 sein darf, wenn man ausschließen möchte, dass Flächenelemente generiert werden, deren Flächeninhalt 0 beträgt (siehe hier). Dies wäre genau dann der Fall, wenn isovalue = value ist, der Isowert also genau dem Wert des aktiven Voxels entspricht.
In Abbildung 2 (rechts) wurden die benachbarten Face Center Points miteinander verbunden. Wie man sieht, ist die dadurch entstandene Linie zusammenhängend - mit zwei Ausnahmen: Dort, wo aktive Voxel direkt am Rand liegen, endet auch die Isolinie. Damit sie geschlossen ist, muss sie außen um die aktiven Voxel herumgeführt werden. Das lässt sich dadurch erzielen, dass man bei aktiven Voxeln außen am Rand stets noch einen Face Center Point einfügt. Tut man dies, erhält man stets eine geschlossene Isolinie (im Zweidimensionalen) bzw. eine geschlossene Oberfläche (im Dreidimensionalen). In dieser Implementierung werden diese äußeren Face Center Points, sofern sie benötigt werden, stets eingefügt, was bedeutet, dass die Isofläche, die durch den VESTA-Algorithmus generiert wird, nirgends irgendwelche Löcher aufweist. Der Abstand dieser äußeren Face Center Points zum Rand wird durch die Variable borderOffset bestimmt, die über die Methode setBorderOffset explizit gesetzt werden kann. Ein Wert von 0 bedeutet, dass der Face Center Point direkt auf der Position des aktiven Voxels liegt, ein Wert von 1, dass er soweit vom Mittelpunkt des Voxels entfernt ist wie dieser vom Mittelpunkt seines benachbarten Voxels. Wie bei der Variable dislocation ist es notwendig, dass borderOffset niemals 0 ist, wenn gewährleistet sein soll, dass keine Flächenelemente gezeichnet werden, deren Flächeninhalt 0 ist.
Werden alle Face Center Points richtig miteinander verbunden, dann erhalten wir eine Vielzahl von Polygonen, die in ihrer Gesamtheit die gesuchte Oberfläche ergeben. Im folgenden wird zuerst erklärt, wie diese Face Center Points berechnet werden. Auf der nächsten Seite wird dann erklärt, wie diese Punkte richtig miteinander verbunden werden.
Jeder Face Center Point wird in dieser Implementierung durch genau ein struct-Objekt des Typs fcp repräsentiert. In diesem struct gibt es nun zwar ein Vertex-Handle, das die Position des Face Center Points in der Mesh speichert, allerdings - und das ist für das Verständnis dieser Implementation des VESTA-Algorithmus von eminenter Wichtigkeit - wird dieses Vertex-Handle nicht dafür benutzt, zu ermitteln, wie benachbarte Face Center Points verbunden werden sollen. Für den eigentlichen VESTA-Algorithmus ist dieses Vertex-Handle ohne Belang! Erst wenn klar ist, welche Face Center Points zu einem Polygon verbunden werden sollen und dieses Polygon dann auch gezeichnet werden soll, wird auf dieses Vertex-Handle zurückgegriffen.
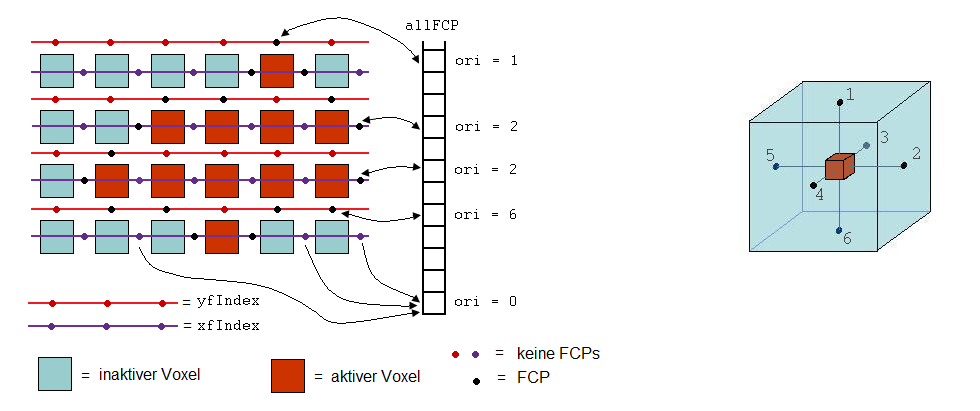
Das bedeutet, dass die für den VESTA-Algorithmus relevanten Informationen über die Lage der Face Center Points anders abgespeichert werden, und zwar mithilfe des int-Werts i, der eine Position innerhalb eines (eindimensionalen) Vektors angibt, und mit dem Wert ori, der angibt, in welcher Richtung von insgesamt sechs möglichen Richtungen der aktive Voxel liegt. Dass diese Art der räumlichen Lokalisierung sinnvoll ist, wird klar, wenn man bedenkt, dass das skalare Feld als eindimensionaler Vektor von double-Werten vorliegt (Abbildung 3 (links)).
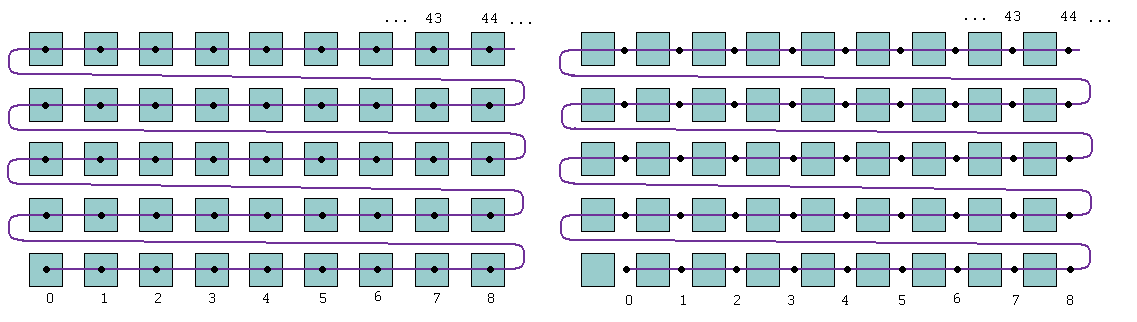
Genauso, wie die double-Werte in einem eindimensionalen std::vector gespeichert und mithilfe der Informationen über die x- und y-Kantenlänge des skalaren Feldes lokalisiert werden können, können auch die Informationen über die Lage der Face Center Points in einem eindimensionalen std::vector gespeichert werden. Auf Abbildung 3 (rechts) sind alle möglichen Positionen eingezeichnet, an denen Face Center Points zwischen zwei Voxeln in x-Richtung liegen können. Darüber hinaus sind am rechten Rand noch mögliche Positionen markiert, die von Face Center Points am Rand eingenommen werden können. Wie man sieht, hat dieser Vektor von Face Center Points genau dieselbe Länge wie der std::vector des skalaren Feldes. Allerdings sieht man sofort, dass mit diesem Vektor von Face Center Points nicht alle möglichen Positionen von Face Center Points abgedeckt werden. Es fehlen die möglichen Positionen zwischen den Voxeln in y-Richtung und natürlich auch die Stellen zwischen den Voxeln in z-Richtung. Ferner müssen auch an allen 6 Außenseiten des Quaders Face Center Points positioniert werden können.
Die Lösung besteht darin, dass man sowohl für die Face Center Points in y-Richtung als auch für diejenigen in z-Richtung einen weiteren std::vector anlegt (Abbildung 4 (links)). Um alle Randpunkte erfassen zu können, werden darüber hinaus auch die Quader-Kantenlängen für diese drei neuen Vekoren künstlich um 2 vergrößert (Abbildung 4 (rechts)).
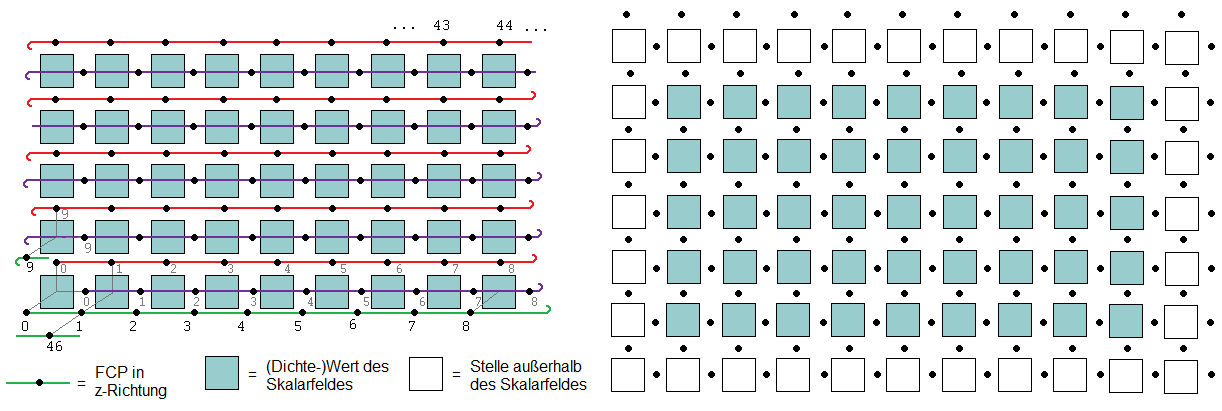
Wie man unschwer erkennen kann, werden mit diesen drei Vektoren alle möglichen Positionen der Face Center Points abgedeckt. Diese drei Vektoren heißen in dieser Implementierung xfIndex, yfIndex und zfIndex und enthalten lauter int-Werte, die auf die Face Center Points verweisen, die in dem std::vector allFCP abgespeichert sind (der int-Wert enspricht dabei dem Index in allFCP). Mit dieser Verweisstruktur wird Speicher eingespart, denn tatsächlich sind die wenigsten Positionen zwischen zwei Voxeln mit Face Center Points besetzt und ein int-Wert kostet weniger Speicher als ein fcp-struct. Ebenso wird Speicher dadurch eingespart, dass für die Positionsbestimmung der Face Center Points nicht ein einziger Vektor verwendet wird, bei dem die Anzahl der Einträge in x-/y- und z-Richtung verdoppelt worden ist, sondern drei verschiedene. Die Ersparnis, die sich daraus ergibt, beträgt ca. 62.5 Prozent und errechnet sich wie folgt: Hat der Vektor des Skalarfeldes eine Länge von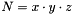 
, so hätte ein Vektor mit doppelt so vielen Einträgen in x-/y- und z-Richtung eine Länge von 
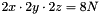, während die drei Vektoren xfIndex,yfIndex, zfIndex insgesamt eine Länge von etwa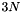 
haben, was nur 
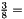37.5 Prozent davon ausmacht. Abbildung 5 zeigt den Unterschied für den zweidimensionalen Fall.
Diese Speicheroptimierung trägt dem Hinweis Rechnung, den Schlei in seinem Paper macht, wo er schreibt: " However, a clear disadvantage is that a large amount of computer memory may be required, in particular, if large amounts of voxels have to be processed. As a consequence, a computer with insufficient RAM may be forced to go into a swapping mode, and the execution time may increase considerably. " (Schlei, S. 10 [1] ) Es hat sich bei diesem Praktikum gezeigt, dass der Speicherbedarf dieser Implementation so gering ist, dass auch die Verarbeitung großer Datenmengen mit den Rechnern am IWR problemlos möglich war: Insgesamt blieb der Speicherbedarf für einen großen Datensatz aus dem ILATO-Projekt bei unter 2 GiB.
Um alle relevanten Informationen über die Face Center Points (im folgenden FCPs genannt) zu berechnen und abzuspeichern, geht der Algorithmus folgendermaßen vor:
Es wird über den Vektor des Skalarfeldes iteriert, der in dieser Implementation mit densities bezeichnet wird und ein std::vector<doubles> darstellt. Dabei wird bei jedem aktiven Voxel geprüft, ob einer seiner Nachbarn inaktiv ist. Falls das der Fall ist, wird ein neuer FCP definiert und in dem std::vector allFCP abgelegt. Gleichzeitig wird in einem der drei Vektoren xfIndex, yfIndex, zfIndex an der richtigen Position der Index abgespeichert, der auf diesen Face Center Point in allFCP verweist. Umgekehrt wird mit i in dem FCP-struct die Position in dem Vektor xfIndex, yfIndex oder zfIndex abgespeichert. Welcher der drei Vektoren der richtige ist, ergibt sich unmittelbar aus der Orientierung des FCPs, die in der Variable ori abgespeichert wurde: Ein FCP links von einem aktiven Voxel hat die Orientierung 5, rechts davon die Orientierung 2, oben entspricht 1, unten der Zahl 6, vorne dem Wert 4 und hinten dem Wert 3 (Abbildung 6 (rechts)). Sobald ein FCP also die Orientierung 2 oder 5 hat, ist die Position in dem Skalarfeld durch den Vektor xfIndex gegeben, falls er die Orientierung 1 oder 6 hat, durch den Vektor yfIndex, und falls er die Orientierung 3 oder 4 hat, gibt der Vektor zfIndex an, wo er sich befindet.
Nachdem über alle Werte des Skalarfeldes iteriert wurde, werden diese vorerst für die Berechnung der Oberfläche nicht mehr benötigt (und spielen nur noch im mixed mode eine Rolle). Zu guter Letzt wird noch ein FCP mit der Orientierung ori = 0 erzeugt, auf den alle Einträge aus den drei Vektoren xfIndex, yfIndex und zfIndex verweisen, an denen sich kein Face Center Point befindet. Damit liegen nun alle relevanten Informationen für die Erzeugung einer Oberfläche in den Vektoren xfIndex, yfIndex oder zfIndex und dem Vektor allFCP, die alle in der Methode fillup erzeugt werden und deren Beziehungen untereinander durch die folgende Abbildung verdeutlicht wird:
Wichtig für alles folgende ist nun, zu verstehen, wie man zwischen den einzelnen FCPs navigieren kann. Wie eben erklärt, kann man von einem gegebenen FCP mittels der Variablen i und ori ermitteln, wo sich dieser Face Center Point befindet: ori liefert einen der drei Vektoren xfIndex, yfIndex oder zfIndex und i die Position in diesem Vektor. Wenn man in x-Richtung nun nach rechts wandern wandern will, addiert man 1 zu i und gelangt damit beispielsweise zu dem Eintrag yfIndex(i+1). Dort findet man dann den Index für den entsprechenden FCP in dem Vektor allFCP. Dieser Face Center Point ist somit der nächste Face Center Point, wenn man in x-Richtung nach rechts wandert. Analog geht man vor, wenn man in y-Richtung einen Eintrag nach oben gelangen will: Dann muss zu i die x-Kantenlänge des Quaders addiert werden, denn das ist genau der Offset, der die Entfernung zu den Face Center Points ausdrückt, die in demselben Vektor eine Ebene höher positioniert sind. Da die Kantenlänge des Quaders aller möglichen FCPs in x-Richtung um 2 größer ist als die Kantenlänge des ursprünglichen skalaren Feldes, beträgt der Offset edge1 = xEdgeLength+2. Ebenso verfährt man, wenn man in z-Richtung genau um eine Position nach vorne oder hinten navigieren will: Man muss den entsprechenden Offset addieren bzw. subtrahieren, nur dass dieser in diesem Fall edge2 = (xEdgeLength+2)*(yEdgeLength+2) beträgt, sich also aus dem Produkt aus x- und y-Kantenlänge ergibt.
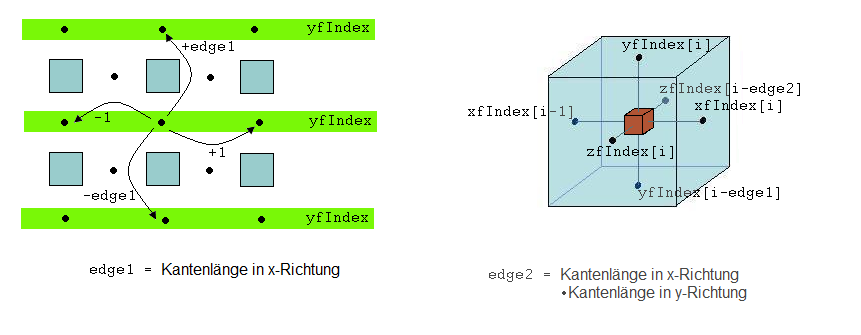
In Abbildung 7 werden diese Zusammenhänge dargestellt. Links sieht man, wie man von einem Face Center Point, der durch eine Stelle im yfIndex-Vektor referenziert wird, zu seinen in x- und y-Richtung benachbarten Face Center Points gelangt. Dabei wird in allen Fällen wieder eine Stelle in yfIndex getroffen. Will man zu den diagonal benachbarten Face Center Points navigieren, muss man jedoch zwischen den Vektoren xfIndex, yfIndex oder zfIndex wechseln. In welcher Beziehung die Indices dieser benachbarten FCPs stehen, sieht man in der Abbildung 7 (rechts). Der rote Würfel in der Mitte repräsentiert einen (Dichte-)Wert des Skalarfeldes. Die unterschiedlichen Offset-Werte, die für die Navigation im Rahmen des VESTA-Algorithmus benötigt werden, werden in den Arrays offsetCube[7][4][3] und doffset[7] abgelegt (die 7 ergibt ergibt sich aus der Anzahl der möglichen Orientierungen der Face Center Points: ori = 1 - 6 und ori = 0). Diese beiden Offset-Arrays werden auch in der Methode fillup erzeugt bzw. mit Werten befüllt.
Einführung FaceCenterPoints Zyklenberechnung Vesta-Zyklen Triangulierung Abstandsgesetz Ergebnisse Ausblick Anwendung Quellennachweise
1.8.6
